対頂角の性質と大きさが等しい理由は？

対頂角は角の位置関係の中でも見つけやすい位置関係です。

錯角や同位角の位置関係にある角は離れていたり、大きさが違ったりするため分かりにくいのですが、対頂角はいつもすぐ隣にあるため見つけやすい位置関係にあります。

対頂角が見つけられないということはあまりないと思いますので、この記事では対頂角の性質となぜそんな性質になるのかについて見ていきます。

まずは対頂角がどのような性質を持っているのか見ていきましょう。

対頂角の性質って

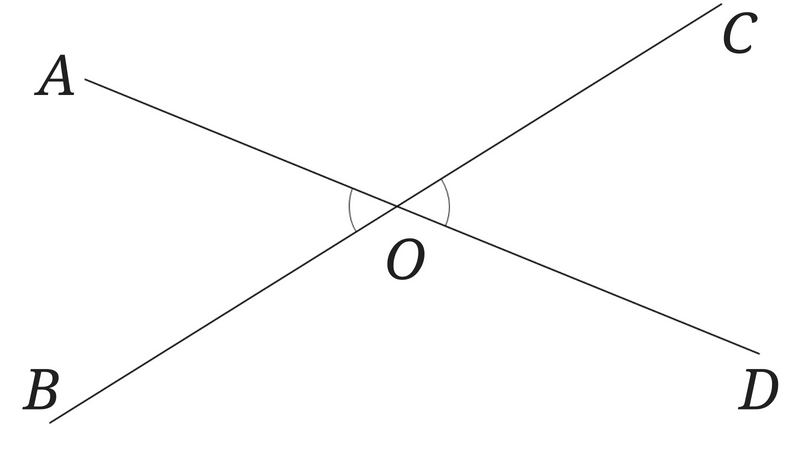
対頂角^[1] … Continue readingは図のような位置関係の角になります。

向かい合った角なので見ただけでも見つけられるのではないかと思います。
位置関係は簡単に分かりますね！
対頂角の大きさは常に等しいと言うことも覚えておきましょう。

上の図の印のある角が等しいことを言うときは
対頂角は等しいので、∠AOB=∠COD
というような感じで書けると良いと思います。

証明の問題や記述の問題では∠AOB=∠CODとだけ書いても減点や不正解になってしまうので、「対頂角は等しいので」のような理由もきちんとつけましょう。
今回は合同な三角形の証明ではないので、対応関係が特にないので∠CODを∠DOCと書いてもOKです。
・合同な図形の対応する角の答え方と対応順

対頂角が等しい理由は？

対頂角が等しいのはなぜでしょう。
対頂角が等しいことを証明してみましょう。
図中の∠AOBと∠CODが等しいことを証明します。

∠AOB=∠BOC-∠AOC･･･①
∠COD=∠AOD-∠AOC･･･②
∠BOC=∠AOD=180°なので
①より
∠AOB=180°-∠AOC･･･①’
②より
∠COD=180°-∠AOC･･･②’
①’と②’の右辺が等しいので
∠AOB=∠CODとなるので対頂角は等しいということになります。

また、式を使わずに図から見て理解することもできます。^[2]証明するように言われたときは前に書いた証明を書くようにしてくださいね。ただ実際にやっていることは先ほどの証明と同じです。

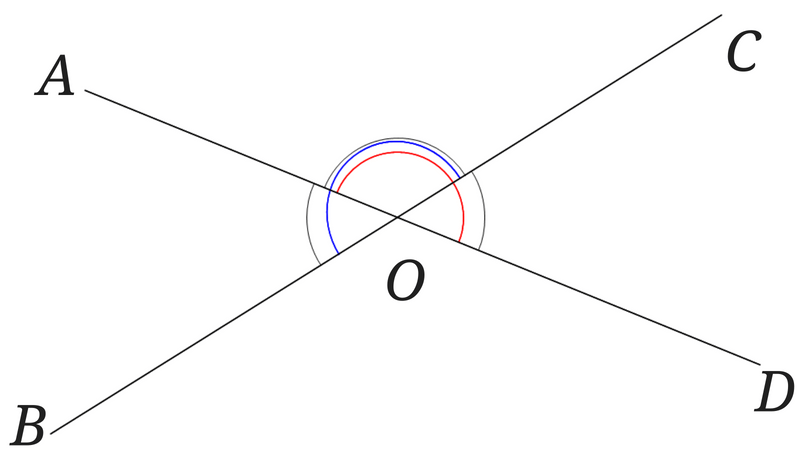
図の中の赤と青の角度はどちらも180°です。
青の部分から∠AOCをひくと∠AOB、
赤の部分から∠AOCをひくと∠COD
だから∠AOB=∠CODといえますね！

対頂角はいつも等しいということが言えました。

まとめ

今回は対頂角の性質と大きさが等しい理由についてでした。
対頂角の位置関係と大きさが等しいということは、すぐに覚えられると思いますのでまずはしっかり位置関係と大きさが等しいということを覚えましょう。
対頂角を角度を求める問題で使うのも証明問題で使うのも難しくないと思います。
いつも隣にありますしね。
ここをつかんでおくと、いいなってポイントは証明です。

∠AOB=∠BOC-∠AOC･･･①
∠COD=∠AOD-∠AOC･･･②
∠BOC=∠AOD=180°なので
①より
∠AOB=180°-∠AOC･･･①’
②より
∠COD=180°-∠AOC･･･②’
①’と②’の右辺が等しいので
∠AOB=∠CODとなるので対頂角は等しい。

と証明をしたのですがココでのポイントは
∠BOC=∠AOD=180°！

このことを①の式と②の式に代入して対頂角が等しいことを証明しました。
記号で書くと、∠BOCと∠AODと違うように見えたものが等しいと言えるようにした点です。
∠BOCと∠AODが、どちらも180°ということを言って代入したところを自分自身でできるようにしておくといいです。
この過程が入ると証明をその証明を嫌がる子が増えるんですよね。

出来る子からすると当たり前に見えるかもしれませんが、証明問題ではこの考え方が入ると正答率が落ちます。
書きにくいですし、めんどくさいですし、難しくなっちゃいますからね。
自分で書いていてもちょっとめんどくさいです。笑
だからこそ差がつくところなので、出来るようにしておくのがおすすめです。

めんどくさくはありますがそんなに難しくはないので、数学がちょっと得意かなって子は是非で証明まで出来るようにしましょう。
・平行線の同位角や錯角が等しいことの証明
・同位角と錯角はどう覚える？