前回の「図形の合同ってどういう意味?裏返してもいいの?」では、合同とはどういう図形のことなのかについて書いてみましたが、覚えてもらえましたか?
簡単に復習しておくと、合同な図形は一方の図形をずりずりっと動かしていって重なるもののことをいうのでしたね。
なんとなく、合同な図形ってどういうことをいうのかは、大体分かったと思うので、あとは自分自身でイメージできるようにしておきましょう。
ちょっと難しいのは、ずりずりっと動かしていっても重ならないものでも合同な図形だといえる場合でした。
一方の図形を裏返して、ずりずりっと動かして重なるものも合同な図形といえましたよね?
あれ?そうだったかな?って子は、もう一度復習しておきましょう。
さて、今回は図形の証明の単元で出てくる「対応する」って言葉について考えていきます。
「対応する辺」や「対応する角」という風に出てきますよね。
書いていることは合っているのに△にされてしまっている(減点されている)ときは対応するって言葉や考え方を適当にしちゃってることがあります。
せっかくテスト勉強を頑張って受けたのにちょっとしたことで減点されるなんてもったいない!
細かすぎ!気にしないでいいじゃん!って思ってしまうけど定期考査ではここがあやふやなせいでほとんどの問題に△がついてしまうことも・・・
そんなことにならないように、「対応する」ってどんなことを言うのかしっかり理解していきましょう!
合同の時の対応する角・辺ってなに?
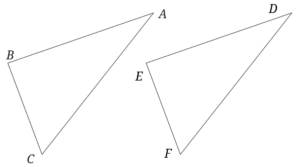
問題文に「△ABC≡△DEF」とあるのでこの二つの三角形は合同ですね。
それではこの問題を使って合同な図形の対応する角や辺について考えていきましょう!
「対応する」って、どういうことか分かりますか?
考えてみると意外と難しいと思います。
実際、なんて書こうか私も迷ってしまいました(笑)
とりあえず、対応するとはどういうことをいうのかを考えていくときは図形を重ね合わせたイメージをもつようにしましょう。
図形を重ね合わせてみて、重なっているところが対応するという関係になります。
例えば、∠Aに対応するのは、Aに重なる点になります。
D、E、Fのどれか分かりますか?
Aに重なる点なので、Dということになります。
なので、∠Aに対応する角は∠Dってことになります。
そんなに難しくないですよね!
それでは、∠CABに対応する角は何でしょう?
きちんと答えを考えて書いてくださいね!
解答は、∠FDEですね。
できましたか?
重なっている通りに書かないと×になってしまうので注意してください。
∠CABに対応する角を書くときに、∠EDFと書くと×になってしまいます。
∠EDFと書くと、点Cに対応する点が点E、点Aに対応する点が点D、点Bに対応する点が点Fという意味になります。
点Aに対応する点が点Dなのは正解だけど、それ以外の点は対応しているとはいえませんよね!
これは2つの図形を重ねてみると明らかです。
対応する通りに書くのはとても大事なので、必ず確認しながら書くようにしましょうね!
2つの図形がずらすだけで重なる場合は、このようにどことどこが対応しているのかを考えるやり方で答案を作ってもそんなに難しくはありません。
けれど、これが図形を裏返して重ねるということになると、急にどことどこが対応するのか見つけるのが難しくなりませんか?

∠CABに対応する角は何でしょうか。
すんなり書けますか?
何も悩まずに書けるのなら図形に対するセンスがあるのかもしれません!
問題は先ほどの<例題1>とあまり変わらないけれど、図は<例題1>と違って一方が裏返しになっていますよね。
裏返しになっているため、頭の中で2つの図形を重ねるのが難しいのだろうなと思います。
私は苦手です(苦笑)
頭の中で上手くひっくり返して重ねるのは難しいですよね。
だけど実は、図を重ね合わせるイメージができなくても、証明を書くときにはもっと簡単に書けるんです!
図形の記号は対応順になっている!
それは問題文中の「△ABC≡△DEF」に注目です。
△ABCと△DEFが合同って書いてありますね!
これはあくまで△ABCと△DEFが合同ってことなんです。
△ABCと△EFDが合同ではありません。
つまり、これは△ABC≡△DEFより、点Aと点Dが、点Bと点Eが、点Cと点Fが対応するってことなんです!
∠CABに対応する角を答えるときには、△ABCと∠CABを比較してみます。
∠CABは△ABCの「後ろ」「前」「真ん中」の順に並んでいますよね?
なので∠CABに対応する角は、△DEFの記号を「後ろ」「前」「真ん中」の順に書いて∠FDEとなります。
ここが分かればすんなり書けるはずです!
実際にもう一題してみましょう!
次は辺CBに対応する辺を答えてみましょう。
できましたか?
図を見ずに△ABC≡△DEFから考えてみましょう。
辺CBは「後ろ」「真ん中」の順番になっています。
△DEFの「後ろ」はF、「真ん中」はEになっているので、答えは辺FEとなります。
辺EFと答えちゃった人は、記号は対応している順番で書くことを意識するようにすると良いと思いますよ。
どことどこが対応しているのかをしっかりつかんでおきましょう。
まとめ
今回は、「対応する」という言葉について、考えてみました。
図形を重ねて考えると分かりやすいですが、図が裏返ってしまうと見た目で判断するのは難しくなりますよね。
問題文中の条件(今回の場合は△ABC≡△DEF)をみて答えると楽に答えられることが多いです。
少しずつ慣れていきましょうね!




