「同位角と錯角の覚え方は?」では同位角や錯角について考えました。
この2つの角の位置関係は証明問題の中ではとっても大事です。
これらを使わずに証明することは不可能な問題が多いと思います。
同位角や錯角は位置関係を示す言葉です。
同位角の位置や錯角の位置は必ず抑えておくようにしてくださいね!
今回はもう少し同位角と錯角について掘り下げてみたいと思います。
同位角と錯角は位置関係を表したものですが、あと1つ条件を加えることで証明問題でもっと使えるようになります。
むしろ、ないと困るくらいです。
同位角や錯角を自由自在に使えるようにして、証明問題が得意になるようにしちゃいましょう!
平行線の同位角は・・・
突然でてきました。
平行線という言葉・・・
ただの位置関係しか示せなかった同位角が、証明のエースに化ける魔法の言葉です。
lとmは平行な直線です。
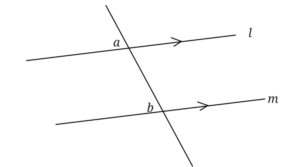
この場合、∠aと∠bの角の大きさは等しくなります。
そのことを平行線の同位角は等しいので、∠a=∠bと書きます。
重要なのは「平行線の」という部分です。
特に模試になると「平行線の」というちょっとした言葉忘れが増える感じがします。
つい忘れちゃったり、そもそも同位角は等しいと思い込んでしまい「同位角は等しいので」と書いちゃったりする子が意外と多いです。
あくまで同位角という言葉は位置関係しか示していないことが分かっていれば「平行線の」を忘れることもなくなります。
「平行線の同位角は等しいので」という1つの言葉として覚えてもいいくらいです。
平行線という条件がついてはじめて、同位角が等しいといえるんですね。
平行線の同位角の証明はどうする?
平行線の同位角の証明をしようとするとなかなかめんどくさいことになっちゃうので(公準とか公理とか・・・)、ここでは「三角形の内角の和が180°」ということを用いて考えていきたいと思います。
平行線じゃない場合をみていきましょう。
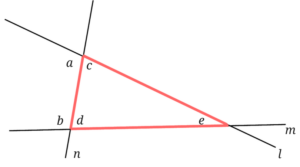
直線nの右側に三角形ができる場合を考えていきます。
平面で3直線がみんな交わっている形ですね。
このときのa+bとc+dに目をつけて考えてきます。
直線nの右側に三角形ができているということは∠cと∠dは三角形の内角、∠aと∠dは三角形の外角になります。
三角形の内角の和は180°でしたよね!
つまり
∠c+∠d+∠e=180°となります。
ということは直線nの右側に三角形ができる場合∠c+∠dは180°より小さいということになります。
∠c+∠dが180°以上になってしまうと∠c+∠d+∠eが180°より大きくなってしまうため三角形といえなくなりますよね。
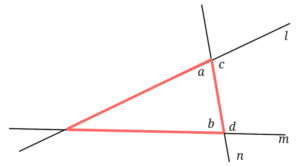
同じように考えると直線nの左側に三角形ができるときは∠a+∠bが180°より小さいということになります。
また
∠a+∠c=180°
∠b+∠d=180°
なので∠a+∠b+∠c+∠d=360°となります。
このことから∠a+∠bが180°より小さい(∠c+∠dが180°より大きい)とき直線nの左側に三角形ができ、∠c+∠dが180°より小さい(∠a+∠bが180°より小さい)とき直線nの右側に三角形ができるということになります。
lとmが平行線の時は、lとmの交点がないため直線nの右側にも左側にも三角形ができません。
ということは、∠a+∠b=180°(∠c+∠d=180°)になります。
それでは平行線の同位角について考えていきますよ。

∠a+∠f=180°・・・①
直線lと直線mが平行なとき、∠a+∠b=180°・・・②
①,②より
∠b=∠f・・・③
よって直線lと直線mが平行なとき同位角は等しい。
証明するとこんな感じになります。
ついでに平行線の錯角にも触れておきましょう!
対頂角は等しいので、∠c=∠f・・・④
③,④より
∠b=∠f
よって平行線の錯角は等しい。
これで、平行線の同位角と平行線の錯角は等しいといえます。
(1つ問題なのは三角形の内角の和の証明の時に平行線の同位角や錯角を使ってしまっているということなのですが・・・笑)
これだと納得できるなーって思ってもらえれば良いと思います!
同位角や錯角を使った問題を解いてみよう。
それでは、実際に練習問題を解いてみましょう。
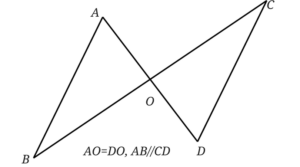
△ABOと△DOCが合同であることを証明してみましょう。
まずはきちんと図に記号を書き込む癖をつけていきます。
文字だけの情報だと条件などに気づきにくくなってしまったり、一体どこが等しくてどこが平行だとかがわかりにくくなることがあるからです。
必ず書き込んでくださいね!
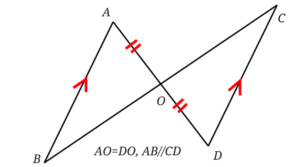
こんな感じになりましたか?
それでは、さらにわかることを書いていきましょう!
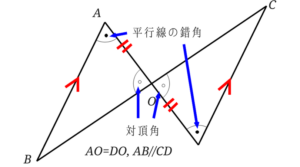
「平行線の錯角」や「対頂角」の文字は書かなくてもいいと思います。
等しい角が書き込めて、合同条件に当てはまれば証明できるということになります。
それでは証明していきましょう。
△ABOと△DCOにおいて
仮定より
AO=DO・・・①
AB∥CDより
平行線の錯角は等しいので、∠OAB=∠ODC・・・②
対頂角は等しいので、∠AOB=∠DOC・・・③
①,②,③より
1組の辺とその両端の角がそれぞれ等しいので△ABO≡△DCOである。
きちんと理由をつけて書くようにしましょうね!
問題文に書いてあることは仮定より○○という感じで書くとOKです!
書き方が分からなくなったときに、もうめんどくさいから、どうせ丸にならないからということで真っ白という子が結構いますがこれは勿体ないです。
これは数学が苦手な子に多くみられるのですが、習っている証明問題の書き方でないとダメだというモノでもありません。
どうしても書けないという場合は、筋道がきちんとしていれば文章でも少なくとも部分点がもらえることがほとんどです。
何か同じ角や辺などが分かるときは書き方が数学らしくなくてもきちんと書くだけは書くようにしましょう。
その書いたことが証明に使う条件であれば部分点になりますよ。
頑張って書いていると証明なんて書けるようになるモノです。
書きたくないという感情に任せていると、解ける証明なのに書かなくなってしまいます。
まずは書かないと部分点も何もありません。
間違いを恐れずにまずは書くようにしましょう。
まとめ
今回は平行線の同位角と錯角についてでした。
「平行線の同位角(錯角)は等しいので」という言葉は図形の証明問題では必ず書くんじゃないかと思うくらいよく出てきます。
同位角や錯角は位置関係を示すだけの言葉で角の大きさが等しい訳ではありません。
あくまで平行線の同位角や錯角が等しいということです。
平行線という条件は必ず書かないとダメなので要注意です!
逆に平行線という言葉を使わずに同位角や錯角という言葉を使うことはまずないので「平行線の同位角(錯角)は等しい」と覚えてしまうと、証明問題などで減点される心配が減っていいかもしれませんね。






「三角形の内角の和が180°」自体が平行線の同位角・錯角をもとに証明されてるので、それを逆に平行線の同位角・錯角に使うことはできないと思います。。
コメントありがとうございます。
おっしゃる通り証明になっていません。
ここを証明するためには、平行線公準をもとに証明すべきだと思います。
しかし、公準は一般的にそこまで知っている方が多いとは思えません。
そのため、三角形の内角の和が180°であることを事実、この公準に準ずるものとして証明してみた次第です。
証明にはなっていないため(公準を使っても同じことになると思います。)、「1つ問題なのは三角形の内角の和の証明の時に平行線の同位角や錯角を使ってしまっているということなのですが・・・」と断りを入れさせていただいております。
ただ、平行線公準を用いて証明することと、三角形の内角の和が180°であることから証明こととの間に大きな差異はないと思います。