角の位置関係ってとっても大切なところなのですが、学校や塾などでもさらっといっちゃうことが多いのではないでしょうか？
1度説明すればもう次からはいけるという子と何度みても分からないという子にはっきり別れる気がします。
対頂角はそんなに難しくないのですが、同位角や錯角の位置関係はなかなか飲み込めないというお子さんは結構います。
合同や証明で何度も何度も使うことになるので、しっかりどことどこが同位角であるのか、錯覚であるの分かるようにしておきたいところです。
入試でもよくでる相似の証明では、角のみを用いることが大半です。
分かりさえすればいいところだと思いますが、分からないというときはしっかり理由をもって分かるようにしておきましょう。
それでは、同位角と錯角の位置関係の見分け方をみていきましょう。
同位角と錯角の位置の覚え方や見分け方は？
まずは同位角の関係からみていきます。
簡単に言うと図のような位置関係です。
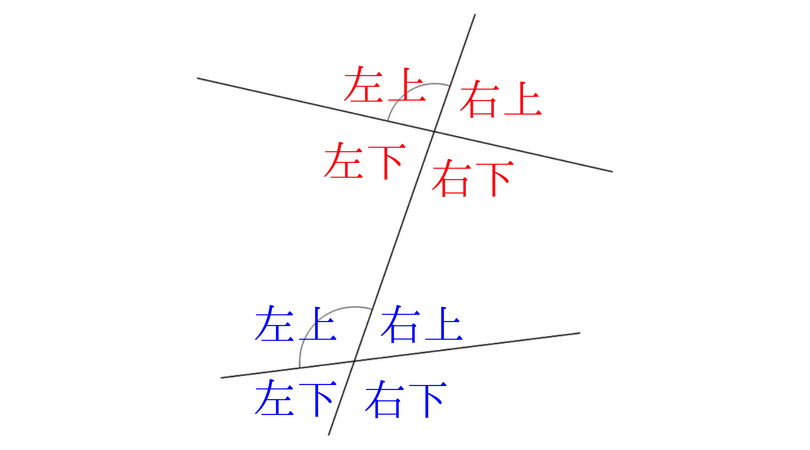
赤字の左上と青字の左上の角に印しを入れています。
こんな位置関係を同位角って言います。
もちろん赤字の左下と青字の左下も同位角になります。
つまりこの図では4組の同位角があります。
分かりましたか？
それでは錯角をみていきましょう。
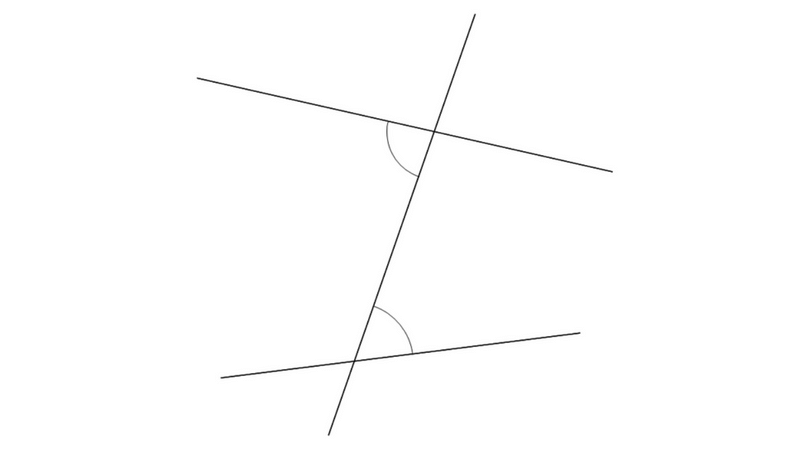
錯角はこんな感じの位置関係をいいます。
同位角と比べるとちょっとわかりにくいですよね？
まずは、横の二直線に注目してみます。
二直線の間を内側、上の直線の上の部分と下の直線の下の部分を外側としましょう！
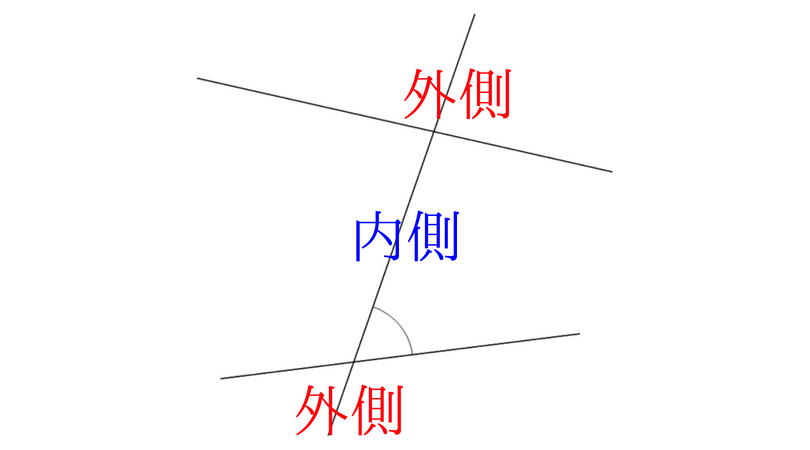
こんな感じです。
錯角は外側の部分にはなく、内側の部分にあります。
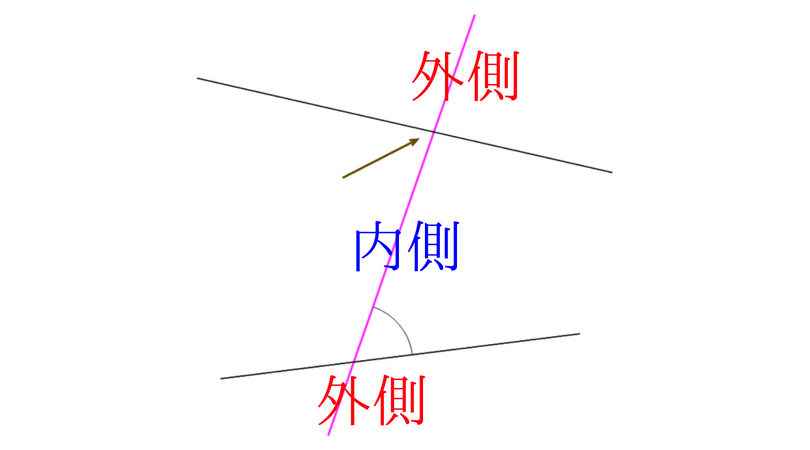
印をつけてある角の錯角は縦の線（ピンク色の線）の反対側の矢印の指してあるところが錯角になります。
色々と説明をしてきましたが、なんとなーく目でみてどれとどれが錯角であるか、同位角であるかがわかれば大丈夫です。
それで見つけることが出来ない場合は、上の同位角や錯角の見つけ方をしっかり覚えておきましょう。
同位角と錯角の問題をしてみよう！
それでは錯角や同位角の見つけ方をちょっと練習してみましょう。
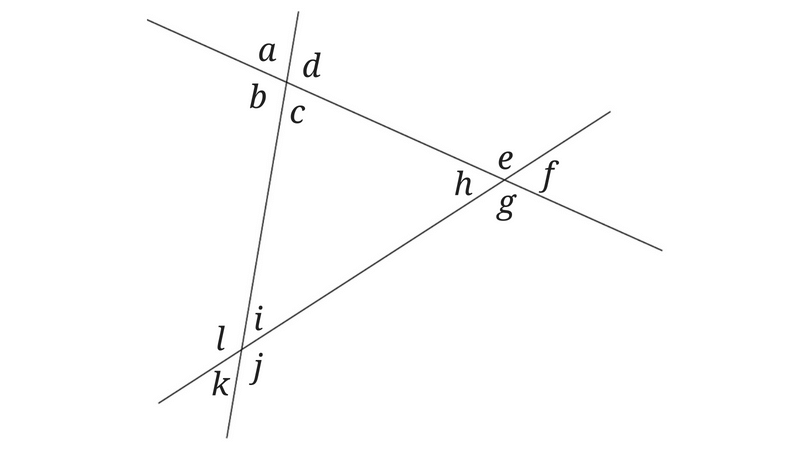
次の問いにa～lの記号で答えてみましょう。
①∠gの同位角
②∠eの錯角
③∠fの錯角
全体を見るとごちゃごちゃになってしまうので、一部だけをみて考えていきます。
①∠gの同位角
左下を隠してみると
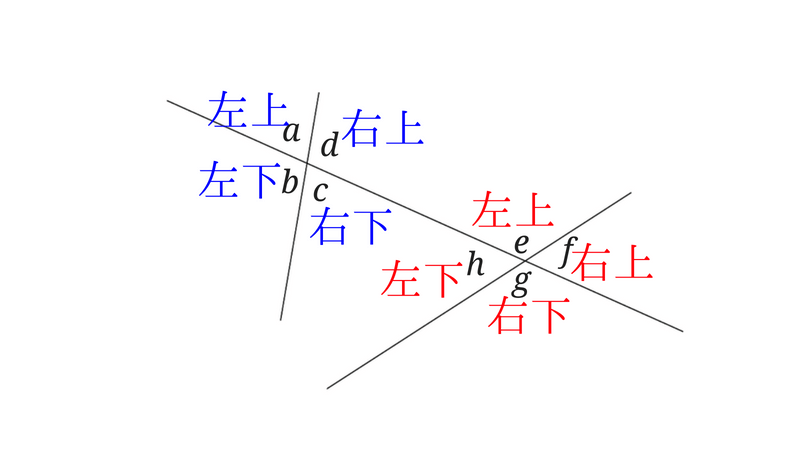
こんな感じになります。
∠gは右下なので同じように右下にあたる∠cが同位角になります。
今度は左上を隠してみます。
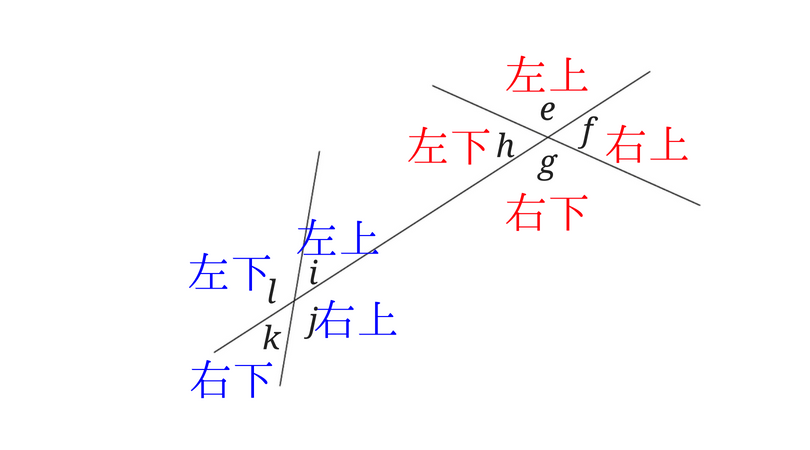
こんな感じになりました。
∠gは右下なので同じように右下にあたる∠kが同位角になります。
答えは∠c,∠kです。
②∠eの錯角
∠eの錯角について考えてみます。
先ほどと同じように左下を隠してみます。
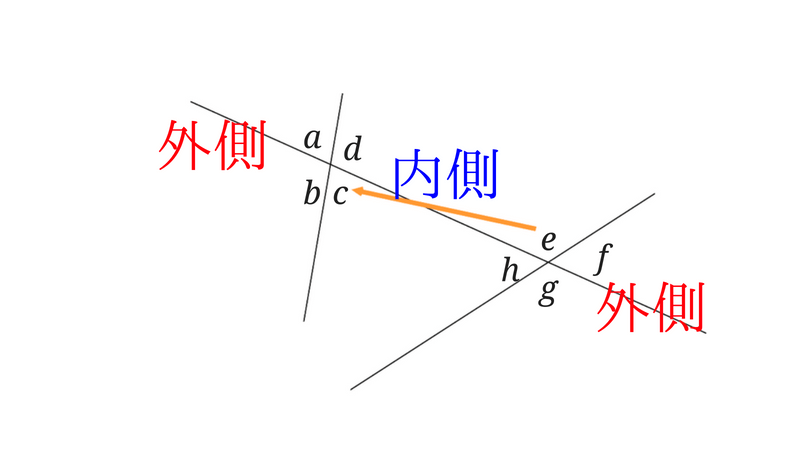
すると∠eは内側にあるので、内側で∠eの反対側にある∠cが錯角になります。
次に左上を隠して考えてみます。
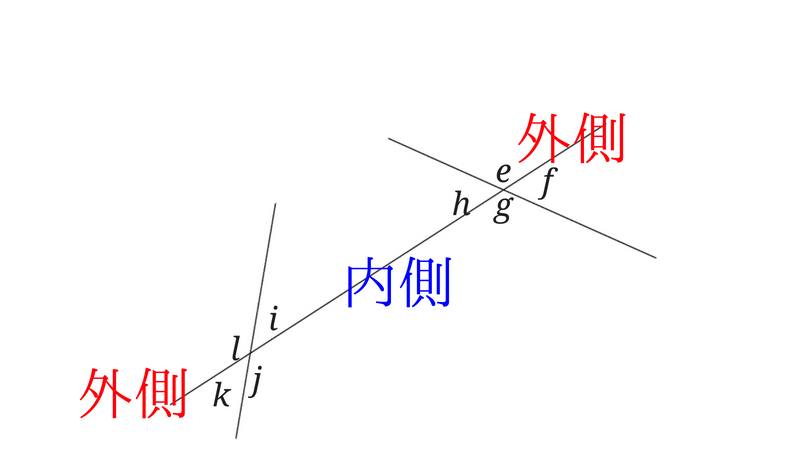このとき、∠eは外側にあるのでこの図の中に∠eの錯角は存在しないことになります。
なので、答えは∠cです。
③∠fの錯角
∠fの錯角について考えます。
③の問題の2つの図を見ると･･･
あれ？どちらの図でも∠fが外側になっていますよね。
ということは、∠fの錯角は存在しないということになります。
よって、答えは、錯角の位置関係にある角はなしとなります。
③は少し意地悪をしてしまいました。
ここで自信を持って∠fの錯角はないと答えられたのならよく考えられているのではないでしょうか。
思った答えが違った人はもう1度見直しをきちんとしておくと良いと思います。
答えがないなんてありえない！と思って適当に角を選んでしまった人！
まずは自分の思ったことを書くと良いですよー！
問題を作った人の意図を考えすぎるとクイズみたいになっちゃいますからね。
まずは自分なりに考えてきちんと間違えることが大事ではないかと思います。
まとめ
今回は同位角、錯角についてでした。
これらは合同や相似などでたくさん使います。
さらっと終わってはしまいますが、これがわからないと証明がわからなくなってしまいます。
きちんと理解してしっかり覚えておきましょう。
同位角や錯角は位置関係を確実に押さえておきましょう。
同位角や錯角の関係にあれば角度が等しいということはありません。
同位角や錯角は位置関係を示す言葉で等しいか等しくないかということに関しては関係がないので注意が必要です。
ちなみに同位角や錯角が等しいといえるときはまた1つ別の条件が必要になります。
それはまたの機会に書きますね。
