以前の記事「約数の総和を素因数分解から求める公式は?」ではある数のすべての約数を足した約数の総和を求めてみました。
約数を全て書き出して足すのは大変ですが、素因数分解をうまく使うと容易に総和を求めることが出来ます。
約数の総和の次は約数の総積を求めてみましょう。
総積はあまり耳にしない言葉ですが、全部の数を掛けた数を意味します。
和でも全て出して計算するのは大変でしたが、それが積ともなるととんでもなく大きな数になってしまいます。
さすがに全ての約数を掛け合わせるのは面倒くさいですよね。
今回は素因数分解を上手に使って総積を求めてみましょう。
約数の全部を掛ける総積を求めよう!
早速、例題を使って1度解いてみましょう!
<例題>
①24の約数の個数を求めましょう。
②24の約数の総和を求めましょう。
③24の約数の総積を求めましょう。
それでは24の約数の個数から求めていきましょう。
24であれば全部書き出して数えても素因数分解からだしてもいいと思います。
元の数字が大きい場合は素因数分解でないと大変なので、どうやって約数を出すかは数字の大小で考えれば良いです。
見て分かる程度であれば全部書き出しちゃいましょう!
今回は、全て書き出す方法と素因数分解を使う方法のどちらもやってみます。
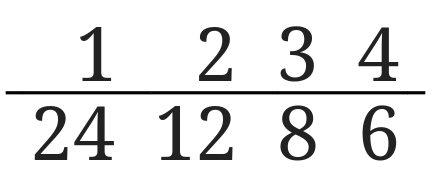
全ての約数を書き出して数えるのであれば図のように真ん中に線を引いて考えるのがおすすめです。
約数は\(1,2,3,4,6,8,12,24\)なので、約数の個数は8個になります。
上の数と下の数を掛けると元の数に戻るのがポイントです。
次に素因数分解を使った約数の求め方でやってみます。
24を素因数分解すると、$$24=2^3\cdot 3$$となります。
よって約数の個数は、$$(3+1)(1+1)=8$$となり、24の約数の個数は8個ということになります。
詳しくは以下のページを見てみてくださいね。
・素因数分解を使った約数の個数の求め方は?0乗が攻略の鍵!
では②の24の約数の総和を求めていきます。
約数の総和を求められる公式から見ていきましょう!
\(a^x\cdot b^y\cdot c^z\)と素因数分解できたときその数の約数の総和は$$(a^0+a^1+\cdots +a^x)(b^0+b^1+\cdots +b^y)(c^0+c^1+\cdots +c^z)$$となります。
詳しくは下の記事を見てださいね!
・約数の総和を素因数分解から求める公式は?
24を因数分解すると、\(24=2^3\cdot 3\)となるので求める約数の総和は求める式は
\( (2^0+2^1+2^2+2^3)(3^0+3^1)\)
となります。
これを解いてみると
\( =(1+2+4+8)(1+3)\)
\( =15\cdot 4\)
\(=60\)
となり、24の約数の総和は60ということになります。
それでは③の24の約数の総積を求めてみましょう。
ここで約数の総積を求める公式を見てみましょう。
ある数\(a\)の約数の個数が\(b\)このとき\(a\)の約数の総積は、
\(a\)の約数の総積\(=a^{\frac{b}{2}}\)個となります。
24の約数の個数は8個だったので、24の約数の総積は$$24^4=331776$$となり331776と言うことになります。
式自体はそんなに難しくないですね。
しかし、なぜ約数の総積をこれで求められるのでしょうか?
考察してみましょう。
なぜ約数の総積はこの公式で求められるの?
ある約数\(a\)の約数の個数が\(b\)個であるときの総積の公式は$$aの約数の総積=a^{\frac{b}{2}}$$でしたね。
なぜこの公式が出来るのかを考えるために、約数の総積を公式無しで解いていってみましょう!
先ほどの例題の24を元に考えてみましょう。
24の約数の総積を\(x\)とします。
すると
\(x=(2^0\cdot3^0)(2^0\cdot3^1)(2^1\cdot3^0)(2^1\cdot3^1)(2^2\cdot3^0)(2^2\cdot3^1)(2^3\cdot3^0)(2^3\cdot3^1)\cdots\)①
となります。
またこれを逆の順番で書いたものも考えてみます。
\(x=(2^3\cdot3^1)(2^3\cdot3^0)(2^2\cdot3^1)(2^2\cdot3^0)(2^1\cdot3^1)(2^1\cdot3^0)(2^0\cdot3^1)(2^0\cdot3^0)\cdots\)②
となりました。
この①と②の2つの式を掛けてみましょう。
\(x=(2^0\cdot3^0)(2^0\cdot3^1)(2^1\cdot3^0)(2^1\cdot3^1)(2^2\cdot3^0)(2^2\cdot3^1)(2^3\cdot3^0)(2^3\cdot3^1)\)
\(x=(2^3\cdot3^1)(2^3\cdot3^0)(2^2\cdot3^1)(2^2\cdot3^0)(2^1\cdot3^1)(2^1\cdot3^0)(2^0\cdot3^1)(2^0\cdot3^0)\)
上下に並んだ数を掛け合わせていくと
\(x^2=(2^3\cdot3^1)(2^3\cdot3^1)(2^3\cdot3^1)(2^3\cdot3^1)(2^3\cdot3^1)(2^3\cdot3^1)(2^3\cdot3^1)(2^3\cdot3^1)\)
\(x^2=24\cdot 24\cdot 24\cdot 24\cdot 24\cdot 24\cdot 24\cdot 24\)
約数を小さい方から並べた数と大きい方から並べた数を順番に掛けたとき、それぞれが24になります。
なので
\(x^2=24^8\)
\(x>0\)なので
\(x=24^4\)
\(x=331776\)
となります。
このことから、ある約数\(a\)の約数の個数が\(b\)個、\(a\)の約数の総積を\(x\)とすると\(x^2=a^b\)となるので\(x=a^\frac{b}{2}\)ということになります。
理屈そのものはイメージしやすいので導き方も覚えておくといいですね!
まとめ
今回は約数の総積についてでした。
解き方そのものはそんなに難しくありませんが、全く知らない状態で初見で解くとなるとちょっと難しいかもしれませんね。
約数を全て小さい数から並べたものと、大きい数から並べたものを掛け合わせるとそれぞれが元の数に戻ってしまううのがポイントです!
求められるだけではたまにしか見ない公式で忘れやすい分、きちんと理屈まで覚えておきましょう!




