以前の「素因数分解を逆さ割り算を使ったやり方でやろう!」の続きになります。
素因数分解を学んでもいまいちメリットが分からない。
問題で素因数分解するようにと書いていれば素因数分解をするけどだから何?
みたいに思っていませんか?
実際これだけでは、やらなくてもいいんじゃない?と言われてしまいそうです。
でも素因数分解はとっても役に立ちます。
今回は素因数分解の利用方法を1つ紹介しますね。
素因数分解を使った約数の個数を出そう!
今回は素因数分解を使って約数の個数を出してみることにします。
12の約数の個数をもとめるくらいなら全部書き出して数えてしまってもたいしたことにはなりませんが、数字が大きくなっていくと大変。
数字が大きくなれば計算も大変になり、数え間違えることもでてきます。
そんな時に役に立つのが素因数分解です。
素因数分解を使って約数の数を求めるとシュッと簡単に求めることが出来ます。
公式として紹介しても答えは出せるのですが意味が分からないのできちんと理屈からやっていきます。
ちょっと前提として知っておいて欲しいことがあるので寄り道しますね。
0乗ってなに?
指数に関する知識がないと分かりにくいので簡単に指数について説明します。
\(3^2\)←この右上にある小さい2が指数になります。
3の2乗って読んで3を2回掛けるって意味になります。
つまり\(3^2=3\times 3\)といった感じです。
よく\(3^2=3\times 2\)としちゃう子がいるので気を付けてくださいね。
少し練習してみましょう。
<計算してみよう>
①\(2^3\)
②\(5^2\)
③\(3^5\)
実際に計算してみてくださいね。
1つずつやっていきましょう。
①\(2^3=2\times 2\times 2=8\)
②\(5^2=5\times 5=25\)
③\(3^5=3\times 3\times 3\times 3\times 3=243\)
できましたか?
数字の右上にある数字が指数と言って掛ける回数になります。
ではここで意地悪な計算をしてみます。
④\(2^0\)
これはいくつでしょうか?
0?1?2?
なんだか分かりませんね。
\(2^2\)
\(2^3\)
\(2^4\)
これらの意味から考えていきますよ。
\(2^2\)・・・2を2回掛けたもの→\(2\times 2\)
\(2^3\)・・・2を3回掛けたもの→\(2\times 2\times 2\)
\(2^4\)・・・2を4回掛けたもの→\(2\times 2\times 2\)
となります。
ここで1つ疑問が出てきます
\(2^1\)ってちょっと変ですよね。
言葉としては2を1回掛けるという意味です。
一見おかしくなさそうなのですが式にしてみると、
\(2^1=\times 2\)ってなりますよね。
ん??
気付きましたか?
掛ける相手がいませんね。
一体何に掛けているのでしょうか?
これは規則性から考えるとバッチリです。
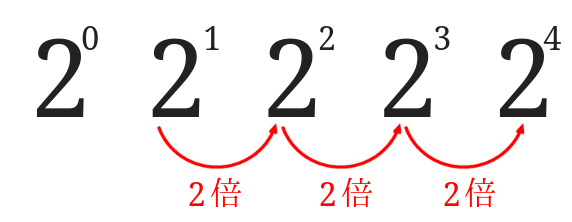
\(2^0\)から\(2^4\)までを書いてみました。
\(2^1\)から順番に2倍ずつになるのは分かりますよね。
2を掛ける回数が1回ずつふえていっているので当然といえば当然です。
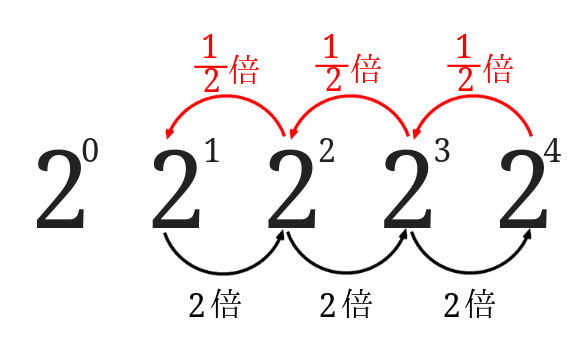
今度はこれを逆に見ていくと\(2^4\)から順番に\(\frac{1}{2}\)倍になっているのが分かりますよね。
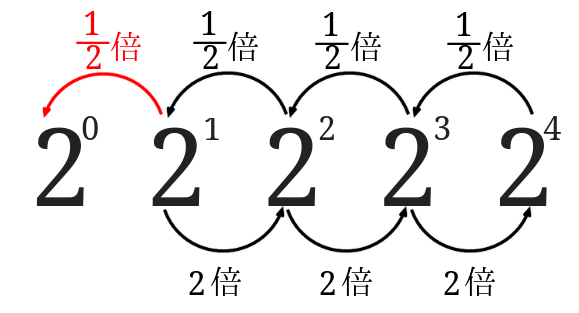
ということは\(2^1\)から\(2^0\)へも\(\frac{1}{2}\)倍して\(2^0\)は\(1\)となります。
規則的な変化が見れると簡単にわかりますね。
つまり
\(3^0=1\)
\(4^0=1\)
といった感じになります。
約数の個数の求め方
それでは約数の個数を求めてみましょう。
\(12\)を例にしてみましょう。
\(12\)を素因数分解すると
$$12=2^2\times 3$$
となります。
\(12\)の約数は\(2^x\times 3^y\)で表されることになります。
\(x\)には\(0,1,2\)がはいり、\(y\)には\(0,1\)が入ることになります。
素因数分解を使って\(12\)の約数をすべて書き出してみると、
\(2^0\times 3^0\)
\(2^0\times 3^1\)
\(2^1\times 3^0\)
\(2^1\times 3^1\)
\(2^2\times 3^0\)
\(2^2\times 3^1\)
となります。
こうやって書き出してしまっては全部数えたことと変わらないのでここで少し見方を変えます。
このときの約数は\(x\)と\(y\)の数字の組み合わせということになります。
\(x\)には\(0,1,2\)の\(3\)通り、\(y\)には\(0,1\)の\(2\)通りがはいるので、\(12\)の約数の個数は、
$$3\times 2=6$$
となるので約数の個数は6個ということになります。
公式として書いてみると、
$$a^x\times b^y\times c^z$$
という形に素因数分解ができたときの約数の個数は、
$$(x+1)(y+1)(z+1)$$
となります。
\(a,b,c\)は素数じゃないとだめなところがポイントです!
ここが素数でない数字になっているときはこの公式は成り立たないのであくまで素因数分解したときにしか使えないことを覚えておいてくださいね!
まとめ
今回は素因数分解を使って約数の個数を求めてみました。
素因数分解さえできれば約数の個数そのものは簡単に求めることが出来ます。
理屈が分かれば場合の数のような感じで求めることが出来ます。
もし試験中に分からなくなってしまったときは全部書き出してしまうのが早いです。
どうやってやるんだったかなーって、試験中に悩んじゃうくらいなら開き直って全部書き出しちゃいましょう。
極端な数字が出題されない限りは数えた方が早かったりします(笑)
高校生の場合はさらに約数の総和を求めさせられることがあります。
すべて約数を書き出して個数を数えるまではそうでもないですが、すべて足してしまうのはさすがに骨が折れます。
小学生や中学生はそこまで必須ではないと思いますが、概念そのものは十分理解できると思いますし、なかなか役立ちます。
高校生は必ずできるようにしておかないと困っちゃうのできちんと理解して、解けるようにしておきましょう。
約数の個数が求められるようになったら約数の総和も求めてみましょう。




