逆さ割り算を使った素因数分解のやり方

素因数分解ってなんとなーくいつ習ったのかはっきりしない単元（？）です。

小学校の倍数や約数で習ったような習わないような…

素因数分解そのものは小学校で扱ってもその先をきちんと教わっていないことがほとんどなので、素因数分解そのものを知っていたとしても全くそのメリットが分からない子がほとんどです。

一応今は中学3年生で正式に習うことになっていますが学習塾に通っていて小学6年生で習ったという子も多いのではないでしょうか。

倍数や約数を習った時に教わっても結局割り算をさかさまにしたもの^[1]逆さ割り算なんて呼ばれたりします。で公倍数や公約数を求めた子が多いと思います。

しかし、これでするとなかなか応用しづらいのが難点。

2つの数の間ではやりやすいのですが、これが3つ、4つとなると理屈的にはかなり難しくなります。

特に公倍数の方は逆さ割り算ではやりにくく感じます。

応用も効きませんし、他の問題形式には対応できず公倍数や公約数は独立した別物として扱わざるを得なくなってしまいます。

今回は素因数分解の基礎的なことから素因数分解を用いた公約数や公倍数の求め方を考えてみたいと思います。

素因数分解とは？

素因数分解をやってみる前にまずは用語からですね！
用語が分からないと何言っているのかなーってなっちゃいます。
それでは用語から見ていきます。

まずは素数からです。
素数っていうのは、
$$2,3,5,7,11$$…のような数です。

上の数の共通点は分かりますか？？
正の約数が2つのみの数です。
それぞれ約数を書き出してみると、
$$2…1,2$$
$$3…1,3$$
$$5…1,5$$
$$7…1,7$$
$$11…1,11$$
のようになり、みんな正の約数が2つしかありません。
こんな数を素数っていいます。

素数でよく間違えるのが\(1\)です。
よく\(1\)を素数にしちゃう子がいるのですが、\(1\)は約数が\(1\)の\(1\)つしかないので素数じゃないですよ。
素数は正の約数が\(2\)つの数です。
間違えないようにしてくださいね。

こういうことを書くと手っ取り早く\(1\)を素数じゃないって覚えちゃう子がいますが、そんな風に覚えちゃだめです。
そんな風に覚えてもどうせ忘れるだけ。
覚えるのは「素数は正の約数が\(2\)つの数」ってことですよ。
なので、\(1\)は正の約数が\(1\)の\(1\)つしかないから素数ではないと判断できればばっちりです。

次の用語は因数です。
因数は例を見ると簡単なのでそれで覚えてください。
\(6=2\times 3\)
と書けますよね？
このときの\(2\)と\(3\)を\(6\)の因数といいます。
かっこよく言うと「整数をいくつかの自然数の積で表したときその1つ1つの数をもとの数の因数」って言います。

今回のメインの素因数分解は、「自然数を素数の積に分解すること」を言います。
つまり、
$$12=4\times 3$$
これは4が素数ではないので素因数分解とは言いません。
$$12=2^2\times 3$$
これはすべて素数の積で表せたので素因数分解と言えます。

素因数分解のやり方！

それではいよいよ素因数分解のやり方をみていきます。
素因数分解はある数があってそれを素数の積に分解すればいいだけです。
極端な話、見て分かればそれをそのまま書けばいいだけですね。

ただ数字が大きくなると見ただけで素因数分解をするのは困難になってきます。
そこで登場するのが逆さ割り算です。

逆さ割り算というのは割り算の筆算の記号をさかさまにしたものです。
素因数分解をするときには有力なツールとなります。
適当に見てするのもいいですが、意外と便利なので使ってみてくださいね。

逆さ割り算を使った素因数分解のやり方！

実際に\(12\)を逆さ割り算でしてみると、下のように割り算の逆さまになったような記号を書きます。
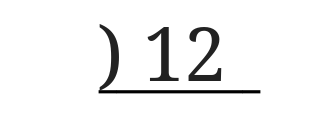12は2で割れるので2を左側に書きます。

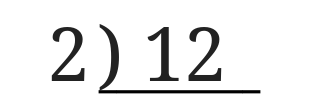\(12\div 2=6\)なので12の下に6を書きます。
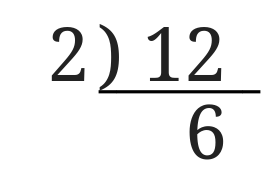さらに6はまだ素数ではないので、割り算の記号を逆さまに書きます。

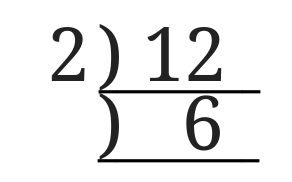
2で割れるので2を左側に書きます。

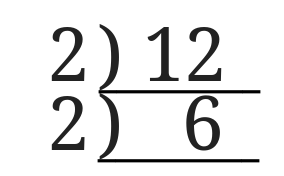
赤丸の部分の３が素数になったのでおしまいです。

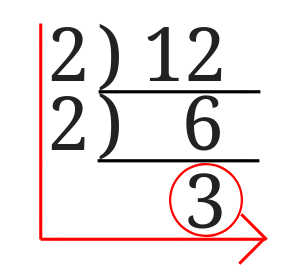
左側と1番下の数をかけると12になります。
つまりこんな風になります。
$$12=2^2\times 3$$

ポイントは素数で割り続けることですね。
素数じゃない数で割っちゃだめですよ。
素因分解じゃなくなっちゃいますからね。

まとめ

今回は素因数分解のやり方などについて扱いました。
まずは素因数分解の用語をきちんと覚えることが先決です。
中間考査や期末考査のような定期考査では用語そのものもよく出題されますしね。

数学が得意な子でも用語の問題は意外と盲点となるので、きちんと数学が得意な子もきちんと覚えておいてくださいね。
もちろん数学が苦手な子も覚えてね！
用語がきちんと分からないと、問題で答えることが分からないからですね。

今回出てきた用語は、素数・因数・素因数分解の3つです。
素因数分解が分からないという子はあまり見ませんが、素数と因数が分からない子は多いです。
因数が分からなくて困ることは少ないですが素数がどんなものか分からないと\(1\)を素数に入れちゃうことが多くなるので特に素数は大事ですよー。
絶対覚えてくださいね。

今日の内容ではただ素因数分解をするところまでだけなのであまりメリットが伝わらないと思います。
この素因数分解・因数の扱い方は非常に大切です。
直接聞かれることが少なくても計算や考え方で後々大きな（？）影響がありますよ。
地味ですけどね（笑）

素因数分解まとめに行く！