直線でできる基本的な平面、三角形。
色々と奥が深いですよね!
三角形の性質をしっかり覚えておかないと証明の問題で困ってしまうこともあります。
二等辺三角形、直角三角形、正三角形、直角二等辺三角形などの性質も覚えておきたいところですが、今回はそのなかでも基本となる三角形の内角の和について証明していきます。
三角形の性質の中でもすべての三角形に共通する性質です!
証明そのものはややこしくはないので、きちんと理解できるようにしましょうね!
目次
三角形の内角の和が180度である理由は??
三角形の内角の和が180°だということは皆さん知っていると思います。
ただ、なぜ三角形の内角の和が180°なのかを考えると、??となる子も結構いるのではないでしょうか。
1番単純なのは、三角形を実際に作って、角をくっつけちゃう感じでしょうか?


こんな感じですね笑
この方法でも、これで三角形の内角の和が180°といえそうなのですが、これだとちょっとまずいんですね。
確かに切って貼ってみたところの3つの内角を合わせると180°になりそうです。
この三角形では内角の和が180°といってもよいのかもしれませんね!
しかし、実際に作った三角形と違う形や大きさの三角形ではどうなのかというと誤差があったりしてちょっと問題がでそうですね。
例えば正三角形の角の大きさはみんな60°です。
そのため切って角を重ね合わせてみるとみんな角が重なっちゃいますよね。
正三角形は特殊な三角形なので角の大きさが同じなんです。
このことから、三角形の角はすべて大きさが同じであるといっても良さそうでしょうか?
ダメですよね!
正三角形が特殊というだけで他の三角形でもすべての角が同じとはいえないのです。
そこで一般的に証明しよう!ってなるんですね。
では実際に証明してみましょう!
と、その前に、内角って何かについてみておきましょう。
内角と外角の関係って?
内角という言葉のお友達に外角という言葉があります。
まずはこの2つの位置関係を抑えておきましょう。
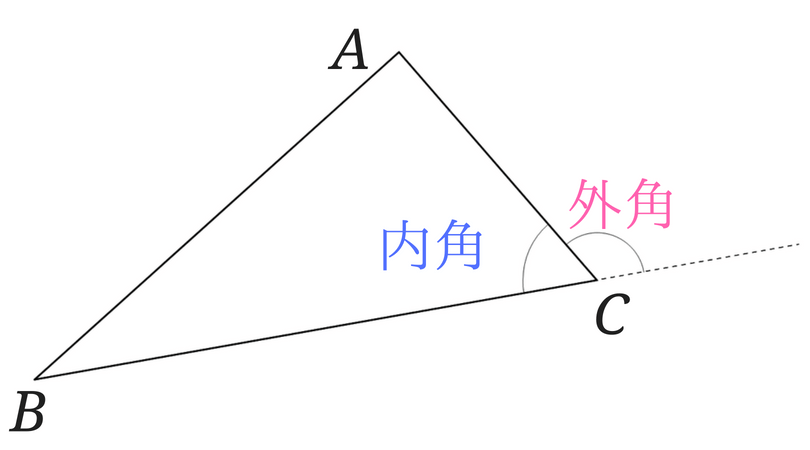
こんな位置関係です。
点線は辺BCを延長したものです。
内角と外角を足すと180°になるというのがポイントですね!
外角という名前から図の外部の角と思って下の図のところが外角と思っている子がたまにいるので、勘違いしないようにしてくださいね!
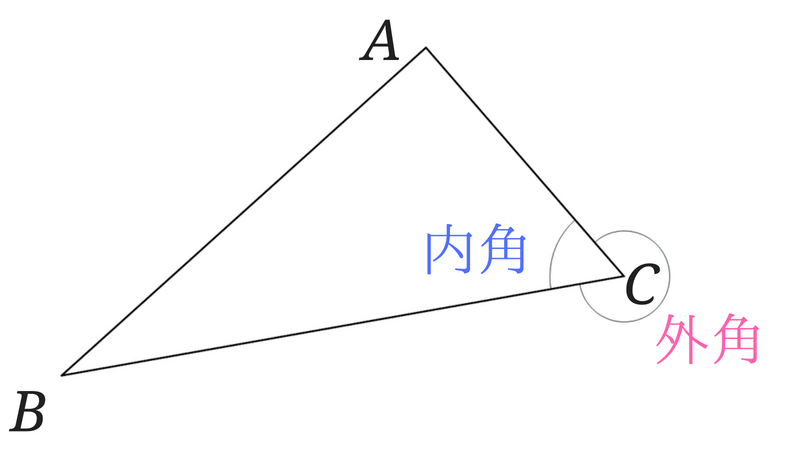
外角から答えを求める問題もあるので、きちんと場所を把握しておきましょう!
それでは三角形の内角の和が180°である証明をしていきます。
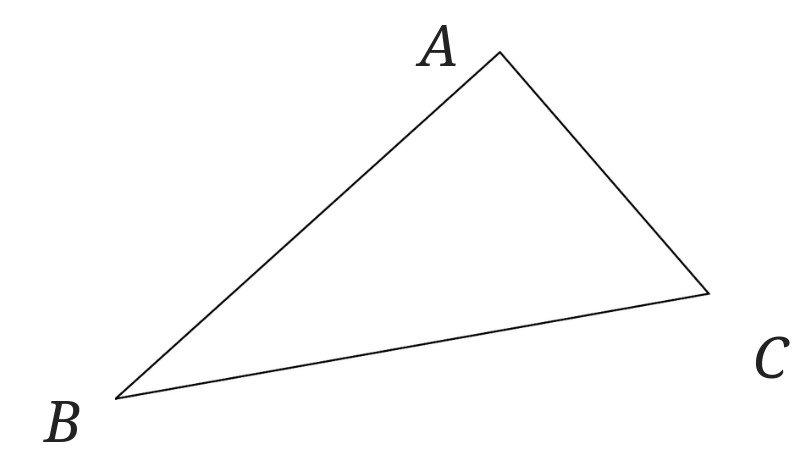
図のような△ABCがあります。
内角の和が180°であることを証明してみましょう!
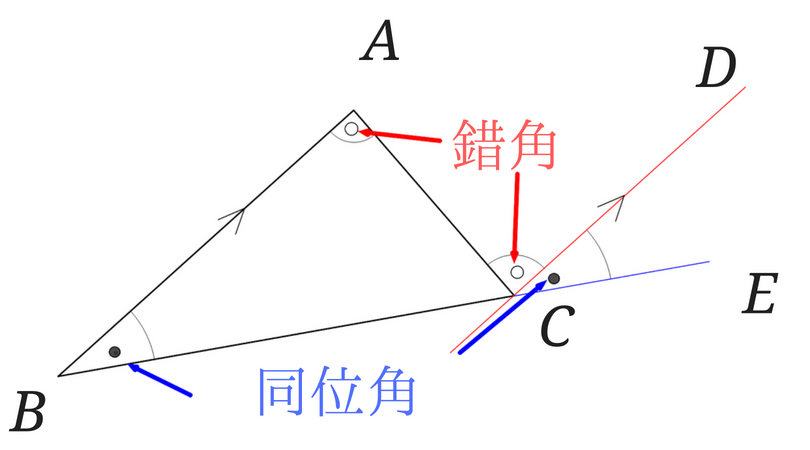
先ほどと同じように辺BCを延長して(青線)、さらに辺ABに平行で点Cを通る直線(赤線)を書きます。
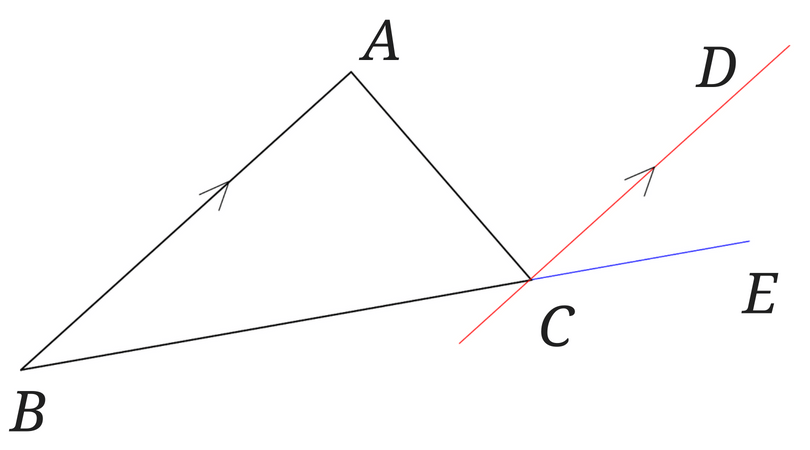
それでは証明していきます。
AB∥CDより
平行線の同位角は等しいので、∠ABC=∠DCE
平行線の錯角は等しいので、∠BAC=∠DCA
よって三角形の内角の和は180°となる。
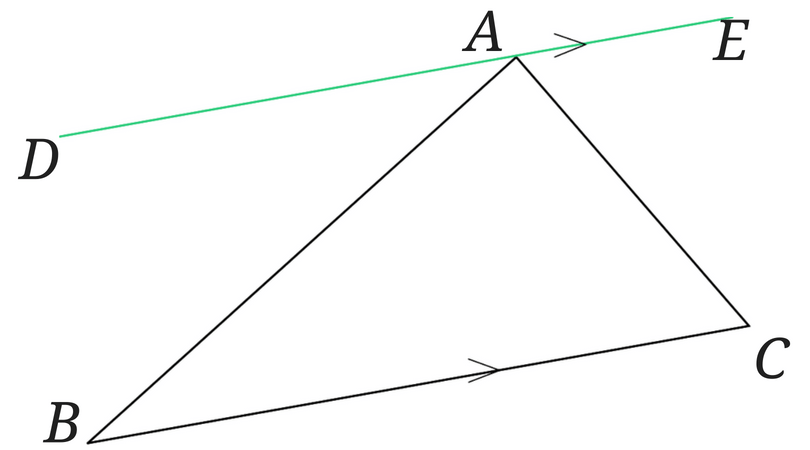
もう1つちょっと違うやり方でしてみましょう。
今度は辺BCに平行で点Aを通る直線(緑線)を書きます。
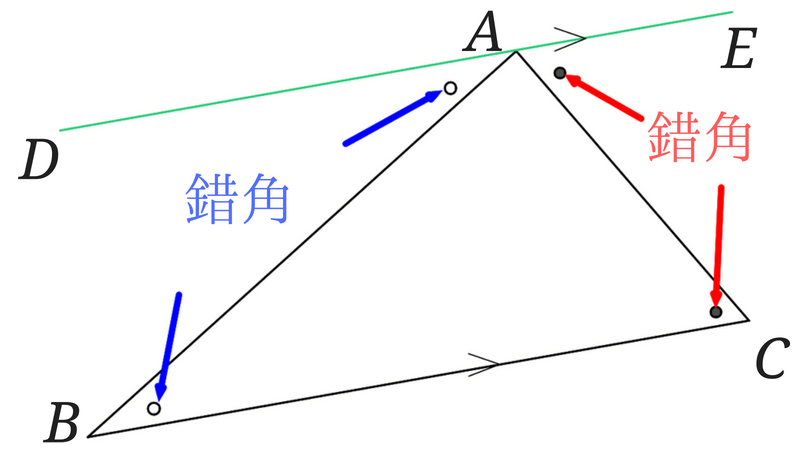
DE∥BCより
平行線の錯角は等しいので、∠ABC=∠BAD
平行線の錯角は等しいので、∠ACB=∠CAE
よって三角形の内角の和は180°となる。
これで三角形の内角の和が180°ってことがいえますね!
多角形の内角の和の公式って??
三角形の内角の和が180°ということが分かりました。
せっかくなので、三角形の内角の和が180°であることを利用して多角形の内角の和を考えていきたいと思います。
まずは四角形から考えていきましょう!
四角形の内角の和が360°である理由
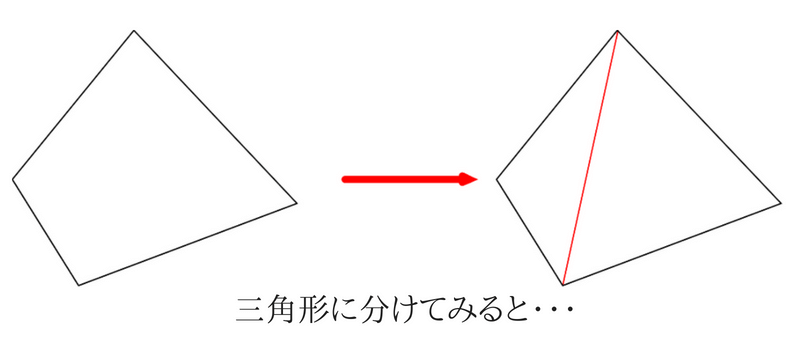
四角形を2つの三角形に分けてみます。
図のような赤線で分けてみると2つの三角形になりました。
ということは、四角形の内角の和は三角形2つ分になることがわかりました。
つまり180°×2=360°になり、四角形の内角の和は360°だということがわかります。
同様にして、五角形と六角形についてもしてみましょう。
五角形の内角の和が540°、六角形の内角の和が720°である理由
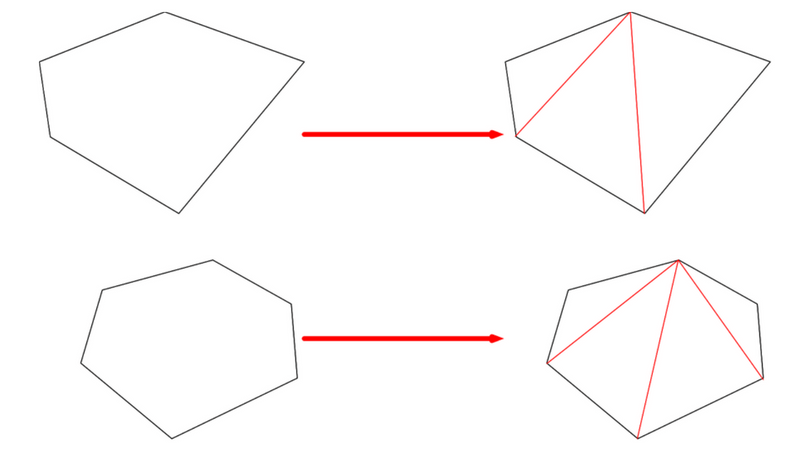
五角形の場合は3つの三角形に、六角形は4つの三角形に分けることができます。
つまり、五角形の場合は180°×3=540°となるので五角形の内角の和は540°、六角形の場合は180°×4=720°となるので六角形の内角の和は720°となります。
なんとなく規則性が見えてきましたね。
三角形の時は三角形が1個
四角形の時は三角形が2個
五角形の時は三角形が3個
六角形の時は三角形が4個
ということは…
これに従うとn角形の時は三角形がn-2個できますね!
三角形がn-2個なので、180(n-2)°がn角形の内角の和ということになります。
ついでに外角の和が360°である理由
n角形の内角の和がわかったので、ついでにn角形の外角の和を求めてみましょう。
となりあった内角と外角の和は180°でしたね!

つまり、すべての内角と外角の和は180n°ということになります。
180n°がすべての内角と外角の和だということは、180n°から内角のすべてを差し引けばn角形の外角の和になります。
式をたてて計算してみると、
180n-180(n-2)=360
よってn角形の外角の和は360°です。
これは何角形であっても外角の和は360°ということで、結構問題を解くうえでなかなか便利なんですよね!
まとめ
今回は三角形の内角の和や多角形の内角の和や外角の和について考えてみました。
n角形の内角の和=180(n-2)
n角形の外角の和=360
ということはきちんと覚えておきましょう。
分からなくなったときは三角形の内角の和から考えていきましょうね!




