今回は中学校で習う三角形の合同条件について考えていきます。
三角形の合同条件の表現の仕方は?
早速合同条件3つを見ていきましょう!
まずは書き出してみますね。
- 3組の辺がそれぞれ等しい。
- 2組の辺とその間の角がそれぞれ等しい。
- 1組の辺とその両端の角がそれぞれ等しい。
中2で習う内容ですが、初めのうちはよく「それぞれ」を書き忘れてしまうので書き忘れないようにしましょう。
三角形の3つの合同条件は丸暗記しないといけないのですが、なぜこの3つが三角形の合同条件なのでしょうか。
なんとなく「三角形の合同条件はこの3つの合同条件にしよう!」と決まったものではないはずです。
三角形の合同条件の証明は?
「2つの三角形が合同条件を満たす→2つの三角形は合同」といえるのはなぜなのか?
なぜあの3つの条件が合同条件に採用されたのか考えていきます。
\(AB=DE\)、\(BC=EF\)、\(\angle ABC = \angle DEF\)とします。
この2つの三角形が合同であることを証明していきましょう。
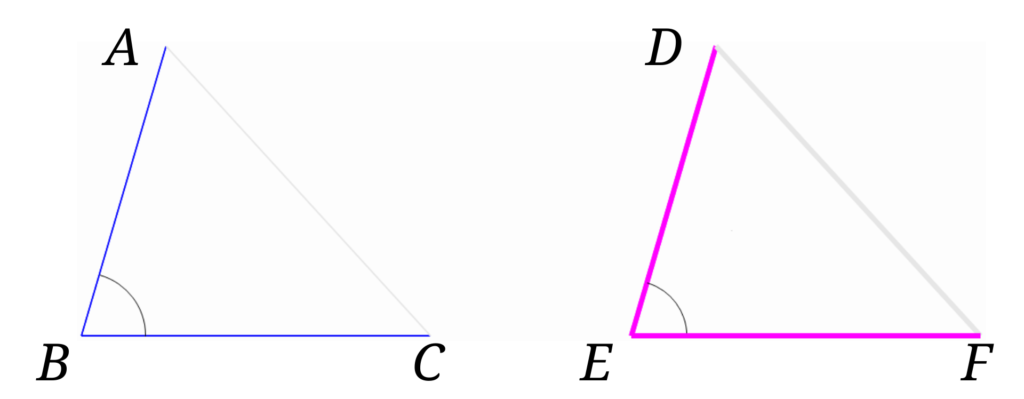
辺\(BC\)と辺\(EF\)が重なるように重ねてみます。
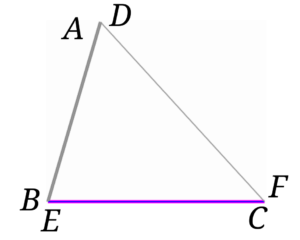
辺\(BC=\)辺\(EF\)なので、きれいに重なります。
次に半直線\(BA\)と半直線\(ED\)を書き入れます。
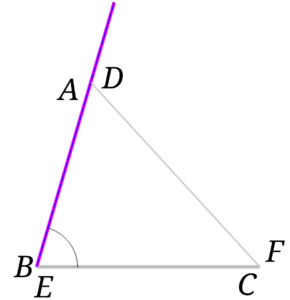
\(\angle ABC = \angle DEF\)なので、2本の半直線は重なります。
\(AB=DE\)となるように、\(A\)と\(D\)をとります。

\(A\)と\(D\)が重なるので、この2つの三角形は合同だと分かりました。
このことから、2組の辺とその間の角がそれぞれ等しい。と、いうことになります。
\(\triangle ABC\)と\(\triangle DEF\)があります。
\(BC=EF\)、\(\angle ABC = \angle DEF\)、\(\angle ACB = \angle DFE\)とします。
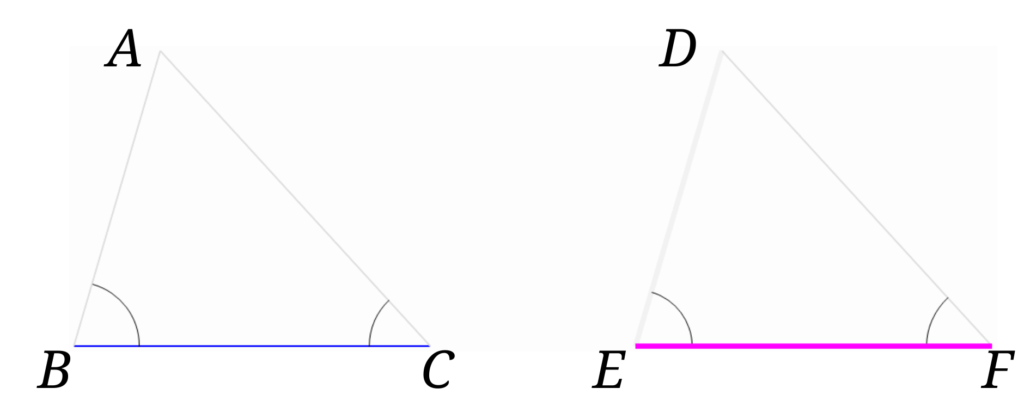
先程と同じように、\(BC\)と\(EF\)が重なるように移動させてみます。
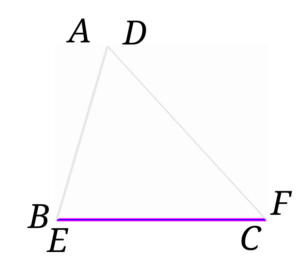
\(BC=EF\)なので、2辺は重なります。
次に半直線\(BA\)と半直線\(ED\)を書き入れます。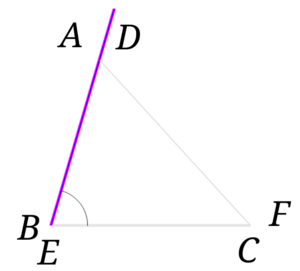
\(\angle ABC = \angle DEF\)なので、2本の半直線は重なります。
次に半直線\(CA\)と半直線\(FD\)を書き入れます。
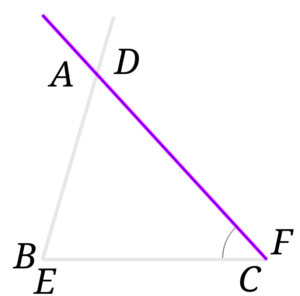
\(\angle ACB = \angle DFE\)なので、2本の半直線は重なります。
半直線\(BA\)と半直線\(ED\)が重なり、半直線\(CA\)と半直線\(FD\)が重なったということは\(A\)と\(D\)も重なるということが分かります。
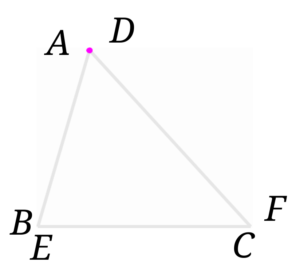
と、いう訳で、1組の辺とその両端の角がそれぞれ等しいときに2つの三角形は合同ということになります。
「3組の辺がそれぞれ等しい」の証明をする前に二等辺三角形の底角が等しい証明をしておきます。
\(AB=AC\)の二等辺三角形を考えます。
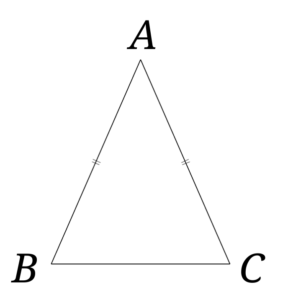
\(\triangle ABC\)と\(\triangle ACB\)において
\(AB=AC\)の二等辺三角形なので、
\(AB=AC\)
\(AC=AB\)
\(\angle BAC= \angle CAB\)
2組の辺とその間の角がそれぞれ等しいので、\(\triangle ABC \equiv \triangle ACB\)となります。
対応する角の大きさは等しいので、\(\angle ABC = \angle ACB\)となり、二等辺三角形の底角が等しいと言うことが分かります。
次に、\(AB=DE\)、\(BC=EF\)、\(CA=FD\)である、\(\triangle ABC\)と\(\triangle DEF\)について考えます。
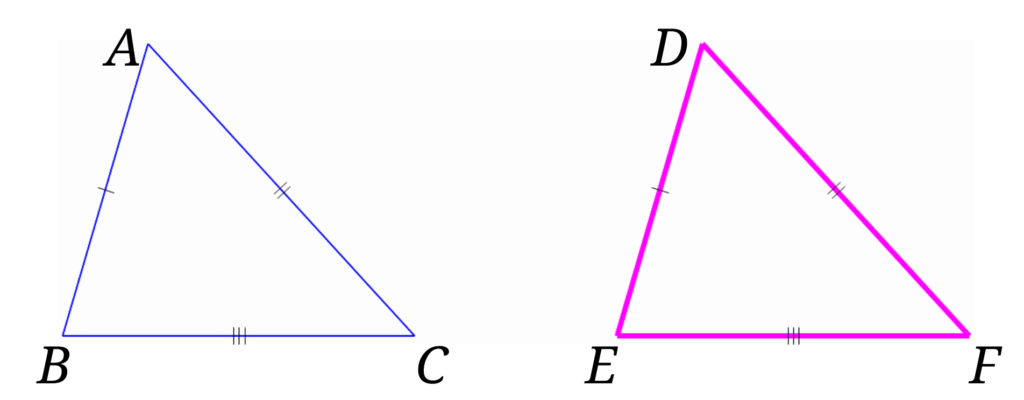
辺\(BC=\)辺\(EF\)を重ねて下の図のように\(\triangle ABC\)と\(\triangle DEF\)を並べます。
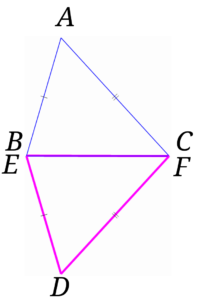
さらに\(A\)と\(D\)を結びます。
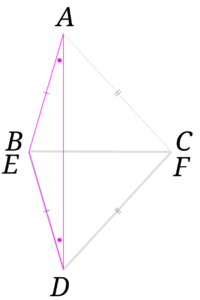 すると、\(\triangle ABD(AED)\)は\(AB=DE\)の二等辺三角形になるので、\(\angle BAD = \angle BDA\)と分かります。
すると、\(\triangle ABD(AED)\)は\(AB=DE\)の二等辺三角形になるので、\(\angle BAD = \angle BDA\)と分かります。
同様に\(\triangle ACD\)についてみていきます。
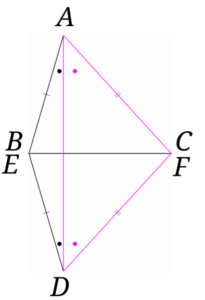
\(\triangle ACD\)は\(AC=DC\)の二等辺三角形なので、\(\angle CAD = \angle CDA\)となります。
\(\angle BAD = \angle BDA\)と\(\angle CAD = \angle CDA\)より、\(\angle A = \angle D\)ということになります。
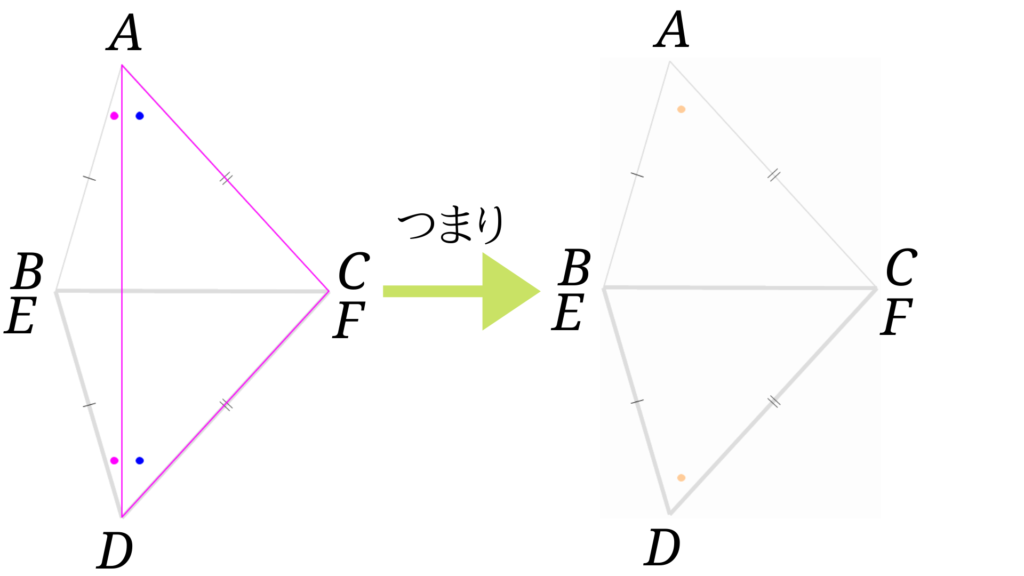
\(AB=DE\)、\(AC=DF\)、\(\angle A = \angle D\)より、2組の辺とその間の角がそれぞれ等しいので、3組の辺がそれぞれ等しいということになります。
三角形の合同条件ってなぜこの3つなの?
中学校の教科書では合同条件はこれらの3つとなっています。
それ以外の条件はないのでしょうか。
なぜ合同条件は3つなのでしょうか。
なぜ三角形の合同条件は3つなの?
三角形の合同条件が3つである理由を考えてみます。
3つの合同条件は3カ所等しいところがあると成立しています。
等しい部分を1カ所のとき、2カ所の時・・・と考えると、これら3つが三角形の合同条件となっている理由が分かりそうです。
等しい部分が1カ所の場合
等しい部分が一カ所の場合考えられる条件は2つです。
- 1組の辺がそれぞれ等しい
- 1組の角がそれぞれ等しい
この条件で三角形を書くと色々な三角形が書けます。
合同とは限らないので、条件が1箇所では駄目そうです。
次に条件を等しい部分が2カ所の場合を考えます。
等しい部分が2カ所の場合
等しい部分が2カ所の場合
- 2組の辺がそれぞれ等しい
- 2組の角がそれぞれ等しい
- 1組の辺と1組の角がそれぞれ等しい
それぞれの条件をもとに合同ではない三角形が書けてしまうので、これらの条件は合同条件になりません。
次に条件を等しい部分が3カ所の場合を考えます。
等しい部分が3カ所の場合
等しい部分が3カ所の場合、角の場所を考えずにざっくり考えると、
- 辺0組、角3組がそれぞれ等しい
- 辺1組、角2組がそれぞれ等しい
- 辺2組、角1組がそれぞれ等しい
- 辺3組、角0組がそれぞれ等しい
の4通りが考えられます。
1つずつ合同条件になりそうかみていきましょう。
3組の角がそれぞれ等しいとき
3組の角がそれぞれ等しいという条件で、三角形を書いてみると色々な大きさの三角形が書けます。
そのため合同条件にはなりません。
三角形の内角の和が180度であることから、考えると2組の角がそれぞれ等しいという条件と同じとも見ることができます。
1組の辺と2組の角がそれぞれ等しいとき
1組の辺の両端の角が等しい場合は、合同条件にあるので、この条件に当てはまらない場合を考えます。
角が2組なので、1組の辺と別の辺の両端の角がそれぞれ等しい場合と角の場所を指定せず単に1組の辺と2組の角がそれぞれ等しい場合を考えます。
1組の辺と別の辺の両端の角がそれぞれ等しい場合
ごちゃごちゃした感じがしますが、図にするとこんな感じです。
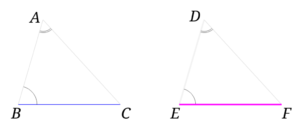
この条件下では、三角形の内角の和を考えると、\(\angle C\)と\( \angle F\)は等しくなりす。
そうなると結局、「1組の辺とその両端の角がそれぞれ等しい」ということと同じ意味になります。
1組の辺と2組の角がそれぞれ等しい場合
図のような場所が等しい場合です。
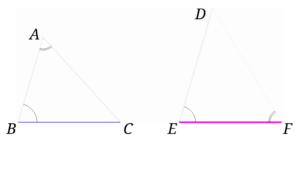
見た目的にも合同ではなさそうです。
また、「2組の辺とその間の角がそれぞれ等しい」という合同条件に合わないので、そもそも合同になりません。
1組の辺と2組の角がそれぞれ等しいときは、「1組の辺とその両端の角がそれぞれ等しい」ときと「1組の辺と別の辺の両端の角がそれぞれ等しい」ときが合同条件と言えそうです。
これら2つの条件は同じことなので、「1組の辺とその両端の角がそれぞれ等しい」の1つを合同条件にしたように思います。
2組の辺と1組の角がそれぞれ等しいとき
「2組の辺とその間の角がそれぞれ等しい」場合を除いて「2組の辺のとその間にない角がそれぞれ等しい」場合が合同になるのかを考えます。
2組の辺とその間の角が等しいという条件がないということは、2組の辺とその間の角が等しくないこともOKということになりるので、合同条件になりません。
3組の辺がそれぞれ等しいとき
これは合同条件の1つですね。
等しい部分が4カ所の場合
- 辺1組、角3組がそれぞれ等しい
- 辺2組、角2組がそれぞれ等しい
- 辺3組、角1組がそれぞれ等しい
1組の辺と3組の角がそれぞれ等しいとき
「1組の辺と3組の角がそれぞれ等しい」という条件は、「1組の辺と2組の角がそれぞれ等しい」という条件と同じ意味になります。
2組の辺と2組の角がそれぞれ等しいとき
「1組の辺と2組の角がそれぞれ等しいとき」や「2組の辺とその間の角がそれぞれ等しい」と同じ意味になります。
3組の辺と1組の角がそれぞれ等しいとき
3組の辺がそれぞれ等しいというところで、合同ということは分かります。
等しい部分が5カ所の場合
- 辺2組、角3組がそれぞれ等しい
- 辺3組、角2組がそれぞれ等しい
2組の辺と3組の角がそれぞれ等しいとき
2組の辺と2組の角がそれぞれ等しいときと同じ意味です。
3組の辺と2組の角がそれぞれ等しいとき
3組の辺がそれぞれ等しいというところで、合同ということは分かっているので、この条件を考えるメリットはありません。
等しい部分が6カ所の場合
- 辺3組、角3組がそれぞれ等しい
究極の条件ですね。
3組の辺がそれぞれ等しいというところで、合同ということは分かります。
こうやってみてみると、4カ所以上の条件を指定すると、3つの合同条件にさらに条件を加えたものもしくは合同条件にならないものとなりそうです。
また、2カ所以下では合同条件になりません。(もし、2箇所の条件だけで合同になるのであればこちらの条件が採用になるでしょう。)
唯一、3つの合同条件と競合しそうなのは下のような場合くらいです。

この条件と、「1組の辺とその両端の角がそれぞれ等しい」という合同条件が競合する感じでしょうか。
結局は同じ意味になってしまうので、「1組の辺とその両端の角がそれぞれ等しい」を採用して合同条件が3つになっているのではないでしょうか。
まとめ
三角形の合同条件についてでした。
- 3組の辺がそれぞれ等しい。
- 2組の辺とその間の角がそれぞれ等しい。
- 1組の辺とその両端の角がそれぞれ等しい。
これらの合同条件はこのままきちんと覚えておきましょう。
きちんと図形で辺と角の位置関係を把握してから覚えてくださいね。
丸暗記するよりも効率がいいと思います。
特に「それぞれ」という言葉は要注意です!
よく忘れるので意識して覚えましょうね!





