図形の合同の意味と裏返った図形

前回の記事「高校受験の数学で証明問題を書けなくて苦手な時はどうする？」では、まずはなんでもいいので書いてみよう！ってことをお話ししました。

図形の証明問題って、何となく嫌でやりたくないなーって、思っちゃいますよね！

特に数学が苦手な子にはそうなのですが、意外と難しくない問題が多いので頑張ってみましょう。

とりあえず、まずは問題文中にある条件をしっかり答案に書くことはしてみましょうね。

白紙だとバツになって終わりなだけですが、少しでも書くと正解でもそうじゃなくても少し進むことができるようになると思いますよ。

少し書いてみるだけで、大きく変わってきます。

めんどくさがらずに頑張って！

今回の記事では、証明をする際の基本について書いていきます。

前回証明問題を苦手をとしている子は、

①何を書けばいいのか分からず全く書けない

②書いてみるけど丸にならない、減点されてしまう

というパターンが多いとお話ししました。

①は心得でなんとかなるのかなーと思うのですが、②の場合ではきちんと書き方を覚えるというよりも、なぜそれを書かないといけないのかをしっかりと理解することが大事だと考えています。

もちろん、書き方は覚えないとだめですけどね！

証明の問題を解く前に、なぜそうなるのか理解をしておくとスムーズに進めていけるようになります。

書き方だけ覚えてもどうやって書くのか分からなくなってしまうので、まずは焦らず我慢して理解できるようにしましょうね！

基本とあなどらず一つ一つ理解しながら覚えていきましょう。

合同な図形とはどういうこと？

合同な図形とはどういうことを言うのか分かりますか？
合同、合同って言いながら、合同ってなに？って、状態だと証明問題ができるようにはなりません。

さらっと流してしまいがちですが、実は1番大事なんですね。
合同な図形とはどんなのものか？どういうことを言うのか？ということを、前回の記事の三角形の合同証明の問題を使って考えていきます。

例題

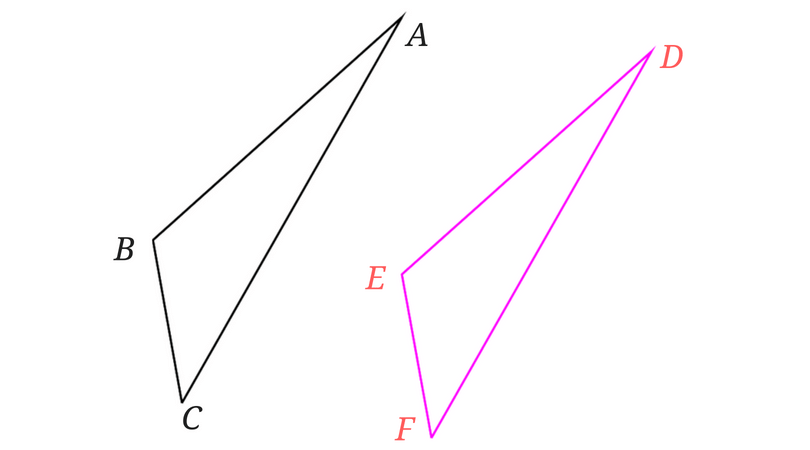
△ABCと△DEFがある。AB=DE、BC=EF、∠B=∠Eであるとき、△ABCと△DEFが合同であることを証明せよ。

こんな問題でしたね。

証明をすると、

△ABCと△DEFにおいて
仮定より
AB=DE…①
BC=EF…②
∠B=∠E…③
①、②、③より、2組の辺とその間の角がそれぞれ等しいので
△ABC≡△DEF

となります。

“証明して合同だと言えれば合同である”という考えだけでは、図をパッと見たときに分からないので、闇雲に証明しないといけなくなってしまいます。
合同な図形というのは、「大きさも形も同じ図形」ことです。

まずは、見た目が同じかどうかを考えて、それから証明して確認するというのが現実的です。
先ほどの合同証明の問題を見た目で合同かどうか検討をつけてみましょう。

<例題1>の図を少しいじってみます。

一方を他方に近づけていくと…

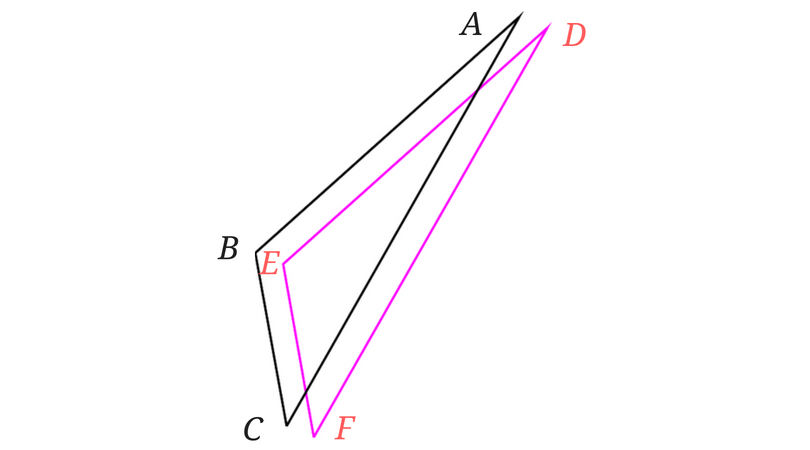
2つの三角形が重なりますね！
こんな感じで重なると合同といえます。^[1] … Continue reading

裏返して重なっても合同？

図をずらしただけでは重ならないけど、裏返すと重なりそう・・・というときはどのように考えたらいいのでしょうか。
そもそも合同なのでしょうか？
合同ではないのでしょうか？

証明を使って合同なのか合同ではないのか判断してみましょう。

次の例題を見てみましょう。

例題

△ABCと△DEFがある。AB=DE、BC=EF、∠B=∠Eであるとき、△ABCと△DEFが合同であることを証明せよ。

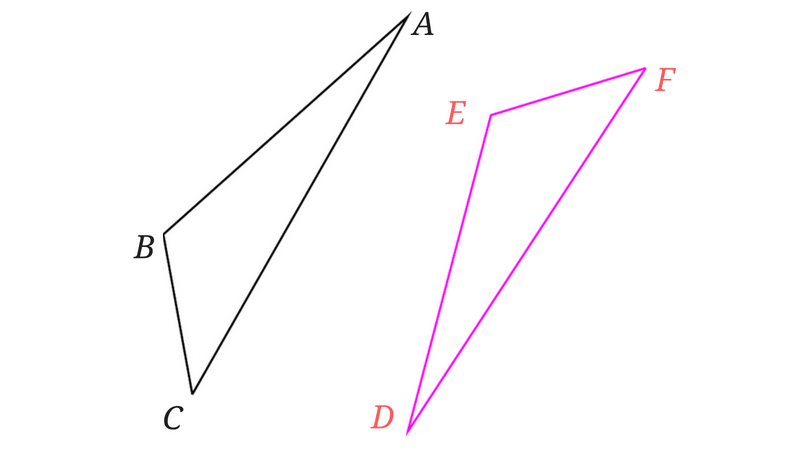
問題文は<例題1>と全く同じですが図が少し違います。
一方の図形を裏返してみました。

合同は、大きさも形も同じ図形なので、2つを重ねてみましょう。
あらら…
重なりませんね…

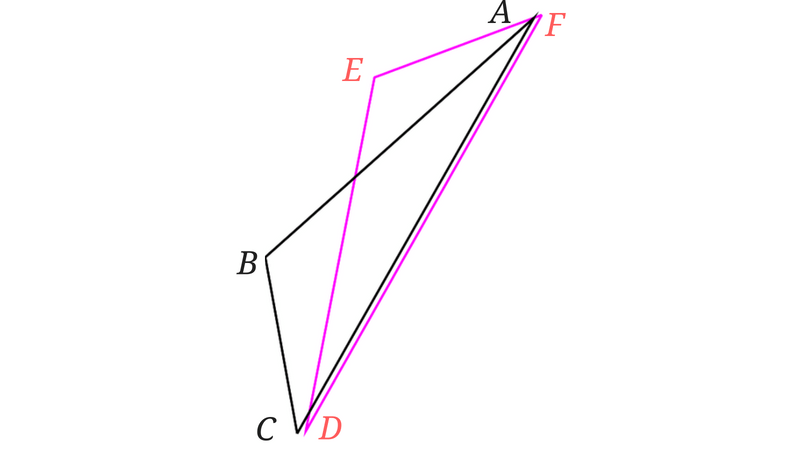
この2つの三角形は合同ではないのでしょうか？
裏返しただけで合同ではなくなってしまうのでしょうか？

どう判断したら良いのか分かりにくいですね。
合同証明ができれば合同な図形と言えるので、合同証明ができるかみていきましょう。

△ABCと△DEFにおいて
仮定より
AB=DE…①
BC=EF…②
∠B=∠E…③
①、②、③より、2組の辺とその間の角がそれぞれ等しいので
△ABC≡△DEF

<例題1>と全く同じように合同って言えてしまいました。
ということは、<例題2>の2つの三角形も合同だということが言えます。
実際、<例題2>の2つの三角形は<例題1>の2つの三角形の一方を裏返したものなので、もう一度一方を裏返して、重ねて見ると2つの三角形は重なります。

つまり、平面上にある2つの図形において、合同だと言えるときには次の2つの場合があると言えます。

合同の意味とは？

①の場合はみんなイメージしやすいので問題ないでしょう。
②の場合は軽く頭に入れておいてくださいね！
合同な図形は形も大きさも同じなので、合同な2つの図形を見つける際には見た目が大きなヒントになります。というか、そのまま見つけられます。

合同証明をするとき、証明する2つの図形が具体的に問題文で指定されてれば問題なくできることが多いのですが、自分で合同な図形を2つ見つけて証明する問題の時に裏返して重なる図形同士が合同であることを知らなければ、どれを証明したら良いのかを見つけることが出来ないということが起こります。

そのため②の一方を裏返してもう一方の図形に重ねることが出来るときも合同だと言うことを意識しておきましょう。
①のずらして重なるタイプの合同は簡単に見つけられますが、裏返されているものって結構見つけにくいんですよね。
見つけにくいけれど、裏返っている合同な図形もあることを頭の片隅においておくと少しは見つけやすくなりますよ。
・高校受験の証明問題が書けないときはどうしたらいい？

まとめ

合同な図形とは形も大きさも同じ図形のことを言います。
合同な図形には、一方をずらしてもう一方の図形に重ねる事ができるものと、一方を裏返してもう一方の図形に重ねる事ができるものとがあります。

見た目で合同かどうか判断しづらいとき、裏返して重なる合同な図形があることを少し意識していると合同な図形は見つけやすくなります。

以上、今回の記事は図形の合同についてでした。

・合同な図形の対応する角の答え方は対応順ってどういうこと？
・三角形の合同条件の表現ってなぜこの3つなの？