連除法(はしご算)を使った最大公約数の求め方と求められる理由とは

最大公約数を求める際によく使うのが連除法や素因数分解。

連除法ははしご算とも呼ばれます。

連除法は中学受験や高校受験、大学受験（？）となかなか幅広く使われますが、何をしているのかちょっとわかりにくい面もあります。

特に3つの数の最小公倍数となると素直に素因数分解をしたほうがいいんじゃないかなと思ってしまいます。

ただやり方を覚えるとすんなりと最大公約数や最小公倍数が求められるのは魅力的！

今回は連除法を使った最大公約数の求め方をみていきましょう。

連除法(はしご算)を使った最大公約数の求め方

それでは早速連除法を使って最大公約数を求めてみましょう。

連除法とは割り算の筆算のときに書く記号をを逆さまにして、次々と\(2\)数のどちらも割り切れる自然数で割っていき、\(1\)以外に\(2\)数を割り切れない自然数がでるところまで割っていきます。
\(24\)と\(84\)を割ってみましょう。
どちらも偶数なのでまずは\(2\)で割ります。

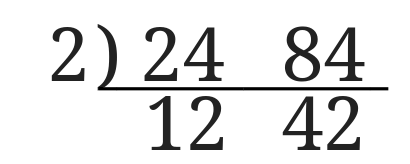
すると\(24\)は\(12\)に\(84\)は\(42\)になりました。
まだどちらも偶数なのでもう\(1\)度\(2\)でわります。

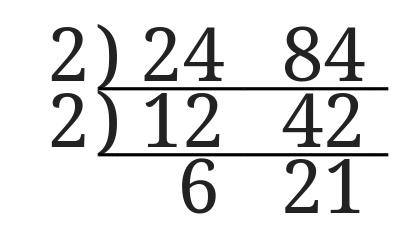
すると\(12\)は\(6\)に\(42\)は\(21\)になりました。
偶数と奇数になったので偶数では割れません。
次はどちらも\(3\)の倍数なので\(3\)で割ります。

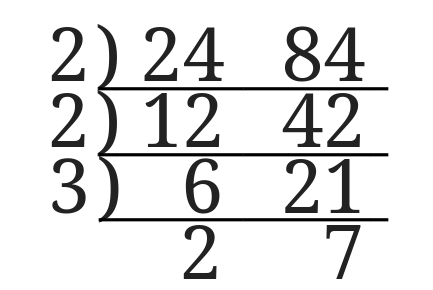
すると\(6\)は\(2\)に\(21\)は\(7\)になりました。
\(1\)以外の同じ数で割れなくなったのでここ終了です。

左側に並んだ数字、今回は\(2\)、\(2\)、\(3\)が並んでいますがこの数を掛け合わせたものが最大公約数になります。

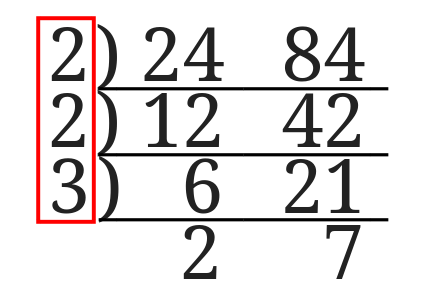
つまり\(24\)と\(84\)の最大公約数は$$2\times 2\times 3=12$$となるので、\(12\)ということになります。
連除法を使って最大公約数を出すことはそんなに難しいことではありませんよね。

今回は素数で割ってみましたが最大公約数を求めることが目的であればもっと大きな数で初めから割ってしまっても問題ありません。
例えば、初めから\(6\)で割れることが分かっている（もしくは割れそうだと思った）なら、いきなり\(6\)で割っても大丈夫です。
先ほどの\(24\)と\(84\)の最大公約数を求める問題を素数ではなく最初に\(6\)で割ってやってみましょう。

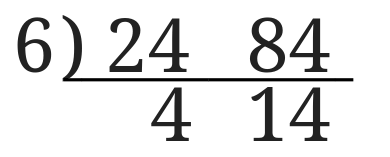
\(6\)で割ると\(24\)は\(4\)に\(84\)は\(14\)になりました。
どちらも偶数なので\(2\)で割ります。

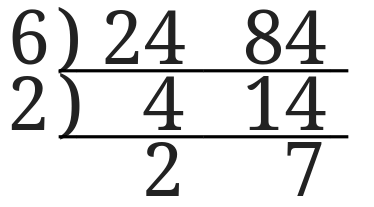
すると\(4\)は\(2\)に\(14\)は\(7\)になりました。
今度は左に並んだ数字が\(6\)と\(2\)になっています。

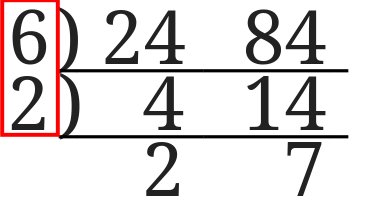
これらの数を掛け合わせると、$$6\times 2=12$$となり素数で割った時と同じになりました。

連除法で最大公約数が出せる理由とは

そもそもなぜ連除法で最大公約数が出せるのかを考えていきます。
まず\(24\)と\(84\)を素因数分解しておきます。$$24=2^3\cdot 3$$$$84=2^2\cdot 3\cdot 7$$

連除法では\(2\)数のどちらもが割れるものを選んで割りますよね。
割り切れるということはその割った数を因数として持っていると言えます。
連除法の左側に並んだ数は\(2\)数がともに持つ因数（共通因数）をくくりだしているということになります。

素因数分解で共通因数を分かりやすいように整理すると$$24=(2^2\cdot 3)\cdot 2$$$$84=(2^2\cdot 3)\cdot 7$$

\(24\)も\(48\)も\( (2^2\cdot 3)\)で割れるということが分かりますよね。
また\( (2^2\cdot 3)\)以外の部分はお互いに割れる数が1以外にない形^[1]こんな2数を互いに素っていいます。になっているので\( (2^2\cdot 3)\)が最大公約数といえます。
・連除法(はしご算)を使った最小公倍数の求め方

まとめ

今回は連除法を使った最大公約数の求め方をしてみました。
やり方を覚えてしまえば最大公約数を求めることは難しいことではありません。
\(2\)数を割り切ることができる同じ数字を探せばいいだけですからね。
しかし、それでは応用などでは使いにくい（そもそも連除法を応用に使うのは難しいかもしれません。）ので素因数分解からも最大公約数を求められるようにしておきましょう。

素因数分解を使って求められればばっちりのはずです。
なぜ連除法で最大公約数が求められるのかが説明できれば文句なしです。

素因数分解まとめに行く！