連除法(はしご算)を使った最小公倍数の求め方と3つの数のときのやり方

今回は連除法を使って最小公倍数を求めてみます。

最大公約数を求めるのは理屈的にもそんなに難しくないのですが、3つの数の最小公倍数を求めるのに連除法を使うとかなり難しくなります。

やり方を覚えるのとともになぜそうするのかは結構な難しさです。

素直に素因数分解でやった方が･･･

今回は連除法を使って最小公倍数を求めてみます。

連除法(はしご算)を使って最小公倍数を求めよう。

早速連除法を使って最小公倍数を求めていきます。

前回と同じ例題を使っていきましょう！

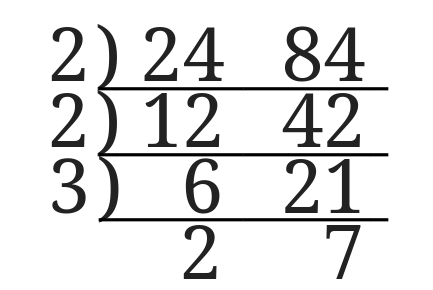
とりあえず\(24\)と\(84\)の最小公倍数を求めてみましょう。
左側の縦に並んだ数字と最後の数字を掛ければいいので、
$$2^2\cdot 3\cdot 2\cdot 7=168$$
となります。

つまり\(24\)と\(84\)の最小公倍数は\(168\)です。

連除法でお互いに割れる数がなくなるまで、割れたら左側の縦に並んだ数と下側の2つの数をかけることで最小公倍数を求めることができます。

連除法(逆さ割り算)でなぜ最小公倍数は求められるの？

それでは連除法で最小公倍数は何故求められるのでしょうか。
例題をもとに考えみましょう。

左側の縦に並んだ数字は\(2\)数のどちらも割り切れる数になりますね。
つまり左側に並んだ数の積は\(2\)数の共通因数ってことになります。
\(24\)と\(84\)を共通因数の部分とそうでない部分に分けてみると、
$$24=(2^2\cdot 3)\cdot 2$$
$$84=(2^2\cdot 3)\cdot 7$$
と書けます。

\( (2^2\cdot 3)\cdot 2\)を因数として含んでいれば\(24\)の倍数といえ、\( (2^2\cdot 3)\cdot 7\)を含んでいれば\(84\)の倍数と言えます。

つまり共通因数の部分と残りの互いにもう割り切れなくなった数(ここの場合は\(2\)と\(7\))を掛けると最小公倍数を求めることができます。
よって\( (2^2\cdot 3)\cdot 2\cdot 7\)で\(24\)と\(84\)の最小公倍数を求めることができます。

\(2\)数の連除法でしていることは次のように考えることが出来ます。
\(2\)数\(a\)と\(b\)の共通因数を\(k\)とすると\(2\)数は次のように書くことが出来ます。
$$a=ka’$$
$$b=kb’$$
\(a’\)と\(b’\)は互いに素^[1]\(2\)数を割り切れる自然数が1のみのこと。例：\(10\)と\(49\)のような関係を互いに素といいます。とします。
この時の最小公倍数は、\(ka’b’\)と言えます。

3つの数の最小公倍数を連除法で求めてみよう！

3つの数の最小公倍数を連除法で求めてみましょう。
3つの数の最大公約数を連除法で求めてもそんなにややこしくなりません。
と、言うのも3つの数の最大公約数を求めるときって、3つの数すべてに共通する因数が最大公約数になるのですが最小公倍数の時はそんなに簡単にはいきません…

連除法で3つの数の最小公倍数を求める前に3つの数\(a,b,c\)の最小公倍数をどうやったら求められるのか考えてみましょう。
\(a,b,c\)を次のように書き換えてみます。
$$a=k_{abc}\cdot k_{ab}\cdot k_{ca}\cdot a’$$
$$b=k_{abc}\cdot k_{ab}\cdot k_{bc}\cdot b’$$
$$c=k_{abc}\cdot k_{bc}\cdot k_{ca}\cdot c’$$
なんだか文字がややこしいですね。
\(k_{abc}\)は\(a,b,c\)の\(3\)つの数の共通因数
\(k_{ab}\)は\(a,b\)の\(2\)つの数の共通因数
\(k_{bc}\)は\(b,c\)の\(2\)つの数の共通因数
\(k_{ca}\)は\(c,a\)の\(2\)つの数の共通因数
\(a’.b’,c’\)は互いに素とします。

するとこの時の最小公倍数は、\(k_{abc}\cdot k_{ab}\cdot k_{bc}\cdot k_{ca}\cdot a’b’c’\)となります。
つまり連除法を使って最小公倍数を求めるには次の手順で求めることができます。

＜例題＞
次の数の最小公倍数を求めよ。
\(660,210, 1386\)

①3つの数全てが割れる数で割っていきます。

660、210、1386の3つの数を割り切ることが出来る2と3で割ります。

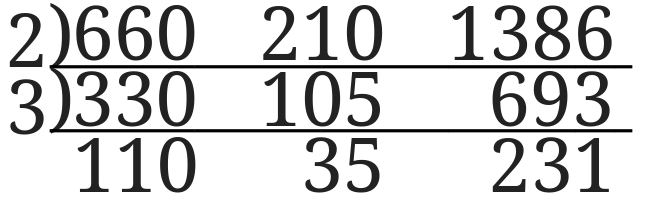
②3つの数全てが割り切れるものがなくなったら2つの数が割れる数で割っていきます。

まずは左の2つの数を割ることが出来る5で割ります。
割り切れない231はそのまま下に書き出します。

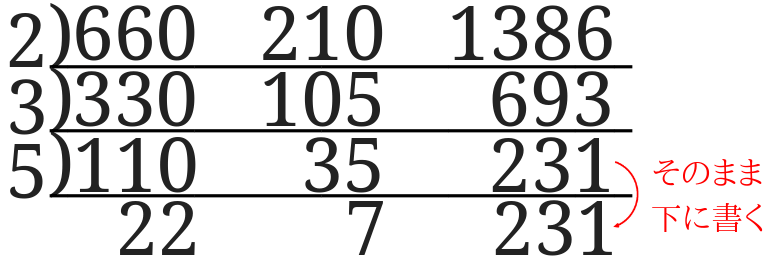
次に35と231 を7で割ります。
22は割り切れないのでそのまま下に書きます。

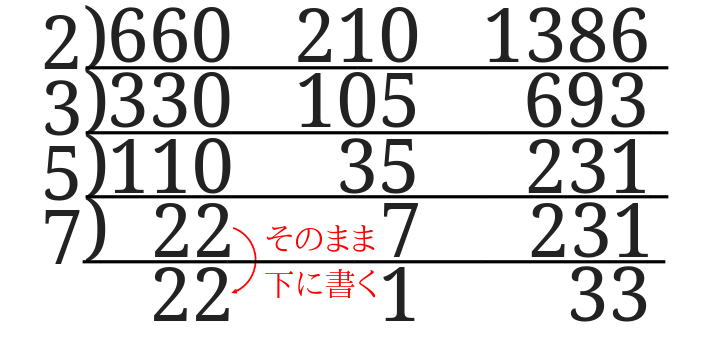
次に22と33を11で割ります。
5は割り切れないのでそのまま下に書き出します。

③2つの数が割り切れる数がなくなったら左側の数と一番下に並んだ3つの数を掛けたら最小公倍数を求めることが出来ます。
この場合だと、$$2^2\times 3^2 \times 5\times 7\times 11=13860$$となります。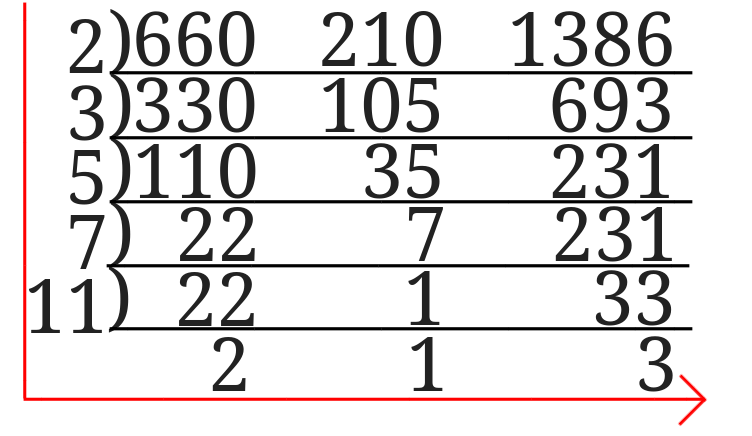

まとめ

今回は連除法を使って最小公倍数を求めてみました。
最大公約数を求めるのに比べると随分と難しいですね。
よほど大きな数でもない限りは倍数を適当に書いていって探すか、素因数分解を使って考えた方が間違いが少ないんじゃないかなと思います。
きちんと理屈まで理解できるようになれば素因数分解や因数の達人といっていいかもしれませんね！

素因数分解まとめに行く！