中学入試で覚えておきたい単位変換

中学入試で出てくる単位を合わせて計算する問題。

単位が苦手な子には嫌な計算問題ですよね。

大人がしても、「めんどくさい」と感じる問題が多いのではないでしょうか。

計算して出せる単位は覚えておく必要ないのですが、暗記していないと全く分からない単位もあります。

この記事では単位の変換の計算の仕方から覚えておくべきものを上げておきたいと思います。

中学入試で覚えておきたい単位変換
まとめ

中学入試で覚えておきたい単位変換

中学受験の単位変換って難しいものです。
覚えておきたい単位変換には、長さ、重さ、面積、体積などがあります。
まずは長さから見ていきましょう。

長さの単位変換

長さの単位は小学校低学年から扱うためなじみ深いのではないでしょうか。
$$1m=100cm$$$$1cm=10mm$$$$1km=1000m$$
これくらい覚えておけば大丈夫です。
長さの単位が分からないという子はあまり見かけないのでそんなに気にしなくても大丈夫でしょう。

覚えられない！覚えにくいという場合は、単位の構成について知っておくとかなり楽になります。
例えば$cm$という単位はセンチとメートルでできています。
センチとは倍率を意味し、メートルとは長さを意味します。
単位は基本的にはこの倍率と何の単位か表す文字で成り立っています。
倍率を覚えておくとのちのち覚えやすくなるのでしっかり覚えておきましょう。
倍率を挙げておくと、
$m$（ミリ）$\frac{1}{1000}$
$c$（センチ）$\frac{1}{100}$
$d$（デシ）$\frac{1}{10}$
$h$（ヘクト）$\times 100$
$k$（キロ）$\times 1000$
これくらい覚えておけば大丈夫です！
他の単位でも使えますよ。

重さの単位

重さの単位もなじみのある単元です。
重さの単位変換もできる子が多いです。
$$1g=1000mg$$$$1kg=1000g$$$$1t=1000kg$$
基本的に単位は1000倍ずつです。
重さはすべて1000倍ずつなのでやりやすいです。

逆に長さの単位でよく使う$cm$は特殊な例といえますね。
他にも$d$（デシ）や$h$（ヘクト）が特殊な例になります。

面積の単位変換

面積の単位変換は今までの単位変換と比べると少し難しくなります。
ただきちんと長さの単位変換ができると計算でほとんど求めることができます。
計算で出せるようにしておきましょう。
まずは$m^2$と$cm^2$の単位変換です。
$1m^2$を$cm^2$に直してみましょう。
$1m^2$は下の図のような正方形です。

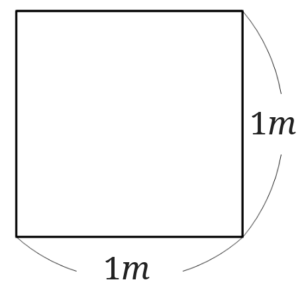
1辺が$1m$の正方形なので1辺を$100cm$と読み替えて面積を出しなおしてみると、$100cm\times 100cm=10000cm^2$となります。
と、言うことは$1m^2=10000cm^2$ということが分かります。
同じように$1km^2$が何$m^2$か考えてみましょう。
$1km^2$は図のような正方形です。

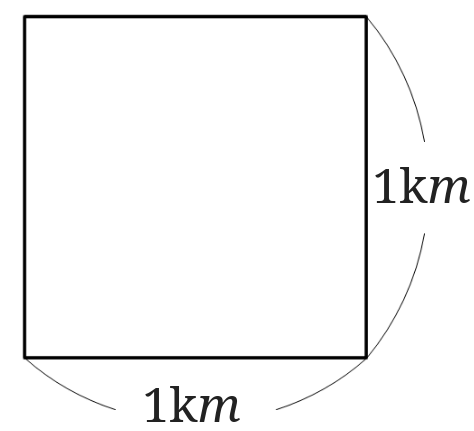
1辺の長さが$1km$の正方形なので1辺を$1000m$と読み替えて面積を出しなおしてみると$1000m\times 1000m=1000000m^2$ということになります。
つまり$1km^2=1000000m^2$ということになります。

ここまでは計算で出せる面積の単位変換をしてきましたが、計算で出せない単位もあります。
それが$a$と$ha$です。

$$1a=100m^2$$$$1ha=10000m^2$$
なのでこれを覚えていればバッチリです。
忘れないようにしましょう。

面積に関しては以下のページで詳しく解説しています。
・面積の単位の意味や読み方とアールとヘクタールの覚え方

体積の単位変換

体積の単位変換は他の単位変換に比べると種類が多いのでやりにくいです。
まずは基本的なところを見ていきましょう。
$$1l=10dl=1000ml$$$$1kl=1000l$$
これは単位の倍率をしっかり覚えていれば大丈夫です。
そんなに必死に覚える必要はないでしょう。
$d$（デシ）がちょっと慣れない倍率なので意識して覚えてくださいね。

次に$m^3$についてみていきます。
ここからは計算で出せるのでシュッと計算で出せるようにしておきましょう。

$1m^3$を$cm^3$に直してみましょう。
$1m^3$は図のような1辺が$1m$の立方体です。

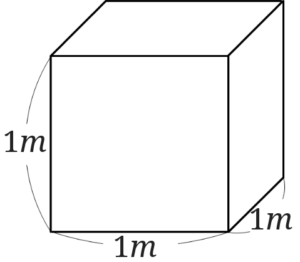
これらの辺の長さをセンチメートルで表すと、1辺の長さが$100cm$の立方体ということになります。
計算してみると$100cm\times 100cm\times 100cm=1000000cm^3$ということになります。
つまり$1m^3=1000000cm^3$ということですね。
数字だけ見ると1と1000000と随分変わってしまうため覚えにくいと思います。
きちんと$1m^3$がどんな立体の体積かを覚えて計算で出せるようにしておくことがおすすめです。

体積の単位変換では絶対に覚えておかないといけない単位があります。
$$1ml=1cm^3=1cc$$
これはきちんと覚えてください。
実際に使う機会はそんなに多くはないのですがこれを知っているか知らないかでできるかできないかが決まってしまうことがあります。
しっかり覚えましょう。