小学生で習う面積の単位には、\(cm^2\)、\(m^2\)、\(km^2\)、\(a\)、\(ha\)があります。
\(1m^2\)を\(cm^2\)に単位を変えると、\(100cm^2\)と書いてしまうお子さんがたくさん。
長さの単位\(cm\)から\(m\)へと変換をもとに考えてしまうため、\(m^2\)から\(cm^2\)のような面積の単位を変換するときよく間違えてしまいます。
公式のように丸暗記してしまってもいいのですがどうしても、しばらくして面積の単位を変換するというときにはどうやって面積の単位を変換をすればいいのか忘れてしまっているということが多いと思います。。
面積の単位がどういうものかが分かれば丸暗記しなくても、別の面積の単位に変えることができるようになります。
ちょっと面倒ですが理由をしっかり理解して覚えることがおススメです。
それでは、面積の単位の意味や読み方やアールやヘクタールの覚え方を説明していきます。
目次
\(cm^2、m^2、km^2、a、ha \)といった面積の単位の読み方とは
面積の単位には\(cm^2、m^2、km^2、a、ha \)があります。
小学生を見ているとそのまま丸暗記している子が多く、理屈を知っている子の方が少ないのではないかと思います。
ちょっと単位の見方が分かったり、見方を理解すると算数だけでなく中学や高校の理科でもとっても役に立ちます。
また、理屈が分かると忘れにくくもなるので、面倒かもしれませんがしっかり理解しましょう!
まずは読み方からみていきます。
\(cm^2\) → 平方[1]ある数を2乗することを平方といいますセンチメートル
\(m^2\) → 平方メートル
\(km^2\) → 平方キロメートル
\(a\) → アール
\(ha\) → ヘクタール
\(a\)と\(ha\)の読み方が特殊なのでこれは覚えましょう。
\(ha\)の\(h\)はヘクトと読んで\(100\)倍という意味です。
素直に読むとヘクトアールとなるのですが、続けて読むとヘクタールになります。
読み方を覚えたら、面積の単位の意味を見ていきましょう!
面積の単位の仕組みを理解して意味をつかもう
\(a\)と\(ha\)は、他の\(cm^2、m^2、km^2\)とは違って特殊なので、\(cm^2、m^2、km^2\)からみていきます。
みんな単位の右上に2という数字がついています。
この記号には見覚えがありますよね。
\(4^2\)のような感じで数字についていることがあります。
4の2乗(にじょう)と読み、意味は4を2回かけるという意味です。
面積の単位の右上についてある数字の2はこの意味と同じ意味です。
\(cm^2\)であれば\(cm\)を2回掛けるという意味です。
つまり\(cm^2、m^2、km^2\)の意味をきちんと書くと、下のような感じになります。
\(cm^2\) → \(cm \times cm\)
\(m^2\) → \(m \times m\)
\(km^2\) → \(km \times km\)
これはどういうことを意味しているのでしょう?
例題を使ってみていきます。
長方形の面積を求めるので、\(2\times 3=6\) となり、答えは\(6cm^2\)です。
この式に単位を付けてみてみると、\(2cm\times 3cm\)となります。
式の単位に着目してみると\(cm\times cm\)となっています。
\(cm\times cm\)を記号を使って書くと、\(cm^2\)となり、面積の単位になっていることが分かります。
逆に、面積の単位から計算式を考えることもできます。
\(cm^2\)の意味は、\(cm\times cm\)なので、cmを2回掛ければ良いことが分かります。
この部分を意識することができれば、\(cm\)を\(m\)にするのを忘れてしまうということがなくなります。
次に面積の単位からどのように計算をすればいいのかを読み取る方法をみていきましょう。
長方形の面積が何\(m^2\)か答える問題です。
求める単位である\(m^2\)は、\(m \times m\)という意味です。
例題2で与えられた長さは\(90cm\)と\(2m\)です。
このまま\(90cm \times 2m\)としてしまうとこの時の単位はあえて書くと、\(cm·m\)ってなってしまいます。[2]単位の意味を理解することで、\(90cm\)をそのまま掛けてはいけないことが分かるようになります。
\(m\times m\)とするには、与えられた縦の長さ\(90cm\)を\(m\)に単位変換をして、\(0.9m\)にします。
そうすれば、\(0.9m \times 2m=1.8m^2\)となります。
単位の意味が分かると単位をみただけで、どんな式を立てればよいか分かるものが多いですよ。
先ほどの例題の求める単位が違うとどうなるかをみてみましょう。
例題2との違いは求める面積の単位です。
例題2では\(m^2\)で聞かれた面積の単位が、例題3では\(cm^2\)となっています。
求める面積の単位から、式は\(cm\times cm\)ということが分かります。
そのため、横の長さの\(2m\)を\(200cm\)になおしてから計算しないといけないことが容易に分かります。
長方形の面積を求めると、\(90cm\times 200cm=18000cm^2\)となります。
単位から計算式を考えることができれば、単位を合わせ忘れるなんてことも減ると思います。
考えれば分かる面積の単位の変換の仕方!
面積の単位の変換って難しいですよね。
数字がとても大きくなるので理屈が分からずに自信をもって答えるのは難しいのではないでしょうか。
例えば「\(m^2\)から\(cm^2\)に単位を変えるときには\(10000\)倍すればいいよ。」
と、教えてあげるとその場では\(m^2\)から\(cm^2\)に単位を変えることができます。
これを教わった子が後々自信をもって\(m^2\)から\(cm^2\)に単位を変えることができることはない気がします。
でもこれも意味が分かればこの\(10000\)倍するっていうことも当たり前のことになりますよ。
それでは、\(1m^2\)を\(cm^2\)に単位を変えてみましょう。
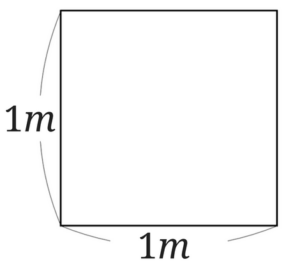
\(1m^2\)は\(1\)辺が\(1m\)の正方形の面積です。
\(1m^2\)を\(cm^2\)に単位を変えると言うことは\(1\)辺が\(1cm\)の正方形がいくつ\(1m^2\)の中に入るかを考えればいいですよね。
\(1m\)は\(100cm\)なので\(1\)辺が\(1cm\)の正方形が縦に\(100\)列、横に\(100\)列並ぶということになります。
つまり\(1m^2\)の中には\(1\)辺が\(1cm\)の正方形が\(100 \times 100\)個、\(10000\)個入ることになります。
よって\(1m^2=10000cm^2\)ってなります。
このように考えると「\(m^2\)から\(cm^2\)に単位を変えるときには\(10000\)倍すればいい」なんてことを覚えなくてもよくなります。
覚えてしまい今後忘れてないというのであれば良いのですが、何度も忘れてしまうという子は理屈をしっかり理解し覚えてみてはどうでしょう?
アールとヘクタールってどんな面積の単位?
\(a\)と\(ha\)はちょっと見た目から違うので仲間はずれにしてきましたが、ここで登場してもらいましょう。
\(1a=100m^2\)
\(1ha=100a=10000m^2\)
となります。
覚えてね!って終わってしまっては覚えにくいですね。
なぜこの単位は登場するのでしょうか?
直接\(a\)と\(ha\)を考えてもなぜか分からないので、\(m^2、km^2\)に登場してもらいます。
\(1km^2=1000000m^2\)ですね。
\(1km^2\)って\(1\)辺が\(1km\)の正方形です。
\(1\)辺が\(1m\)の正方形がいくつ入るか考えてみると、縦に\(1000\)列、横に\(1000\)列並びますよね。
\(1km=1000m\)だから当然ですね。
ということは\(1km^2\)の中には\(1m^2\)の正方形が\(1000\)列\( \times 1000\)列の\(1000000\)個がはいるってことです。
ここでちょっと想像していただきたいのですが、\(m^2\)は\(1\)辺が\(1m\)の正方形を基準に、\(km^2\)は\(1\)辺が\(1km\)の正方形を基準にしています。
実際の大きさを考えてみてくださいね。
いきなり大きくなりすぎなのかなって思いませんか?
例えば\(0.02km^2=20000m^2\)なんですね。
\(km^2\)では小さくて扱いにくいですし、\(m^2\)だと数字が大きい・・・
この間の単位があればいいなぁってことで\(a\)と\(ha\)は登場します。
\(1km^2=100ha=10000a=1000000m^2\)なります。
先ほどの\(0.02km^2=2ha\)となり扱いやすくなります。
まとめ
今回は面積の単位でした。
単位は意味を考えるとわかりやすくなりますよ。
とくに\(a\)と\(ha\)は忘れやすい単位になります
\(a\)と\(ha\)は\(km^2\)と\(m^2\)の単位の間を埋めてあげる単位だと考えるといいですよ。

\(km^2\)から\(m^2\)に変えると数字上では\(6\)桁変わってしまうので、その間に\(a\)と\(ha\)を使うと考えると分かりやすいのではないでしょうか?



