中学受験の入試問題は小学校で習ったことでは対応が難しいものが多いため、学習塾に通っているのがほとんどだと思います。
そうなってくると親御さんも大変ですよね。
もちろん、学校の宿題に加え、塾の宿題もやったり、学校では習わないことを覚えたりと受験する本人も大変ですが、塾への送り迎えだったり、宿題を見てあげたり、親御さんの負担も大きいのではないでしょうか。
中には、宿題は見るだけに限らず教えなきゃいけないことも…
中学受験の問題って結構難しいですよね。
小学校では習わない公式を使えば簡単だけど、公式を知らないので公式を使って説明しても伝わらないことが多かったり…
だからといって、分からないね〜とあやふやにしてしまう訳にもいかず、本当に困ったものです。
今回はそんな事態に陥ってしまう問題の1つ、約数の個数の求め方について書いていきます。
約数の個数の求め方をわかりやすく伝えられる教え方はあるのでしょうか?
中学受験で出る約数の個数を求める!
数字が小さい数の約数の個数を答えるなら間違いなく書いた方が早いのですが、数字が大きくなると大変になっちゃいます。
約数の個数を計算式で出すやり方を考えてみましょう。
必要な知識を整理してみます。
1、素数って何か。
2、素因数分解の仕方
3、累乗の知識(0乗の知識があると分かりやすくなります。)
これくらいあれば理解できそうです。
素数ってなに?
素数って何かをまずは分かってもらいましょう。
結構数字の概念はめんどくさがる子が多いので注意です。
素数は約数が1とその数字自身の約数が2つのみの数です。
例を挙げると、\(2,3,5,7,11,13,17\cdots\)といった数字になります。
ここで注意しないといけないのは、\(1\)の取り扱いです。
\(1\)の約数は何でしょうか?
\(1\)の1つのみですよね。
素数は、約数が1とその数字自身の2つのみの数でしたよね。
つまり1は約数が1の1つしかないので素数ではないということです。
お子さんに教えるときは1は素数ではない!と教えるよりも、素数は約数が1とその数字自身の2つのみの数だという理解を徹底した方が後々も忘れにくい傾向にあります。
素因数分解の仕方
素因数分解の仕方は連除法[1]逆さ割り算やはしご算やすだれ算と言われることもあります。を使うと楽です。
やり方のみを説明するのは難しいので、試しに\(24\)を素因数分解してみましょう。
連除法を使ってするとこんな感じになります。
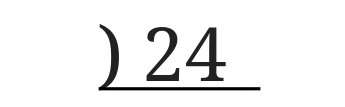
まずは割り算の筆算の記号を逆さまに書きます。
\(24\)は偶数なのでまずは\(2\)で割ってみましょう。
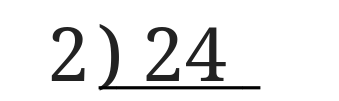
割り算の筆算の左側に\(2\)と書きました。
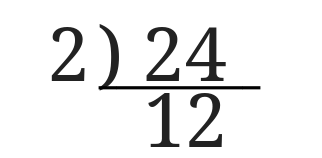
次に\(24\)を\(2\)で割った数\(12\)を\(24\)の下に書きます。
\(12\)は素数ではなないのでさらに続けていきます。
素数になるまで続けていきます。
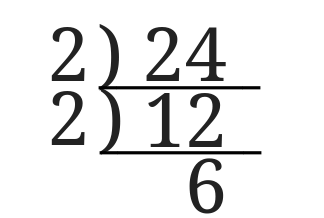
\(12\)は偶数なのでさらに\(2\)で割ってみました。
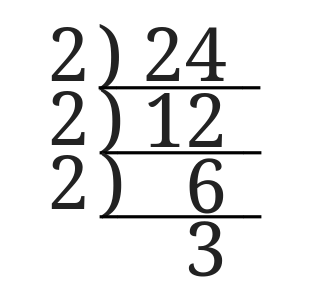
さらにもう1度割ってみました。
すると\(3\)になったのでここで終わりです。
ここで終わりと判断したのは3が素数だからです。
まだ素数でなければ素数になるまで割り続けてくださいね。

矢印の通りに掛けると素因数分解が完了します。
\(24\)を素因数分解すると
$$24=2^3\cdot 3$$
となることになります。
指数の知識(0乗っていくら?)
約数の個数を数えるには指数での表記方法と0乗の扱い方が必要です。
まずに表記方法から見ていきます。
\(2^3=2\cdot 2\cdot 2\)という意味ですね。
左の数を右上の数字の回数掛けたものです。
「5を7回掛ける」と式で書くと\(5^7\)という風になります。
あとは0乗の意味も教えておきましょう。
\(2^3\)というのは2を3回掛けるという意味です。
ちなみに0乗は\(2^0=1\)、\(5^0=1\)といった感じで0乗すると1になります。
詳しくは下のページで確認してください。
・0乗が1になる理由
中学受験向け約数の個数
先ほど24を素因数分解したので24の約数の個数を求めてみましょう!
$$24=2^3\cdot 3$$
でしたね。
24の約数は\(2^x\cdot 3^y\)と書くことができ、\(x=0,1,2,3\)の4通り、\(y=0,1\)の2通りとなります。
つまり\(x\)と\(y\)の組み合わせの通り数の約数の個数ができるということになります。
求める約数の個数は\(4\times 2=8\)となるので、24の約数は8つということになります。
約数の個数を求める公式
公式として書いてみると、
$$a^x\cdot b^y\cdot c^z$$
という形に素因数分解ができるとき、約数の個数は
$$(x+1)(y+1)(z+1)$$
と表すことが出来ます。
\(a,b,c\)が素数ではない数字の時は使えない公式なので注意してくださいね。
まとめ
今回は中学受験の約数の個数の求め方を教えるときに必要な知識についてまとめてみました。
約数の個数そのものを求めるのはそんなに難しいわけではありませんが、前提となる知識がないときは結構大変かもしれません。
丸暗記で乗り越えられるところだとは思いますが、約数や因数などの性質をつかむにはいい問題です。
時間があればしっかり理解してすすめたいですね。
References
| ↑1 | 逆さ割り算やはしご算やすだれ算と言われることもあります。 |
|---|




