勉強って大変ですよね。
高校受験が迫ってきているのは分かっているけどなかなか勉強する気にはなれない…という人も多いのではないでしょうか。
やらないと!という気持ちからとりあえず机の前に座ってシャーペンを握り、ノートを広げ、教科書やテキストを見てみる。
その瞬間、せっかく少しだけ出した”やる気メーター”が一気にマイナスまで下がっちゃった!
5教科ある中でも特に数学ではよくあることでしょう。
少なくとも私はそうでした!!笑
数学が苦手な人にとって数学はその存在意義を疑いたくなるくらい嫌なものですよね!
“なんでこんなことやるんだろう…”って思える問題が多すぎて嫌になります。
しかし、ここは志望校合格に向けて頑張るしかない…!
少しでも数学の点数を楽に上げられるように、今回は証明問題の仕方について書いていきます。
高校受験では数学証明問題が難しい?
高校受験の数学にとって難問となるのはいくつか挙げられますが、図形に関する問題に苦戦している人は多いのではないでしょうか。
図形に関する問題と一言で言っても、面積や長さを求める問題、平行やねじれの位置などの位置関係を答える問題、証明問題などたくさんあります。
さきほど”少しでも点数を楽にあげる”と書きましたが、なぜそれをするのに証明問題を選んだのか。
パッと見、面倒臭いなと思える証明問題、実はそんなに難しい問題ではないんです!
“2つの三角形が合同かどうかなんて見た感じとか、定規を使ってみればわかることを文章にするなんて…やっぱり面倒だし、時間かかるし、この問題は捨ててしまおう!”なんて思わないでくださいね。
難しい計算や公式を使わない証明問題は少しでも書けてしまえば点がもらえるものです!
証明が書けない?!
“証明問題が難しい!”と思っている人は大きく分けると
- 何を書けばいいのか分からず全く書けない
- 書いてみるけど丸にならない、減点されてしまう
という2つのパターンになっているのではないかなと思います。
②のパターンは、別の記事で紹介するので、今回は①のパターンの場合について考えていきます。
証明問題の大きな真っ白な回答欄を見ると焦って何を書けばいいのか分からなくなったり、書く気をなくしてしまったりしませんか?
とりあえず何か書きましょう!と言われても”何を書けばいいの!”って思いますよね。
何を書けばいいのか分からなくて困っているのに何か書いて!と言われても・・・
でも、ここであきらめないで!
意外と”書く”ことにこだわらずに、口頭で質問していくと解答欄を埋められるような答えが普通に出てくるものです。
逆に、条件が何一つ出てこないというほうがレアケースだといえるでしょう。
なぜ口では言えるのに紙には書けないのでしょうか?
1番の理由は言葉にこだわりすぎていることにあります。
自分ではそんなつもりはなくても、教科書や学校の先生が黒板に書く証明と同じように書こうとしすぎているのかもしれません。
まずは言葉の表現を気にせずに書いてみましょう。
もしかすると、せっかく書いたのに学校のテストや模試などで大きく減点されたり、丸ごとバツになって点が取れなかった…ということもあるかもしれません。
とりあえず最初のうちは”書く”ことが大切なので、あまり気にせずどんどん書いていきましょう。
もしそれが、丸をもらえる回答でなかったしても証明で必要とされる内容が書けていればOKだと思います。
初めからきれいな言葉でなんて書けないものだ!というくらいの強気な開き直り具合で大丈夫!!
丸がもらえなくても、学校の先生が見て”丸にはできないけど書いていること(言いたいこと)は分かる!”というくらい書けていればよいと思います。
きちんとしたきれいな答案を書くのはそれからです。
証明が苦手でも、とりあえず書く!
それでは、”とりあえず書く!”ということを目標にして、早速、例題にチャレンジしてみましょう。
今回はあくまでも”書く”ことが目標だということを忘れずにやっていきましょうね!
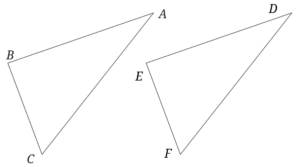
まずは自分なりに紙に書いてみてください。
う~ん、むずかしいな~…って思った人は問題をみながら、条件を箇条書きにしてみましょう。
AB=DE
BC=EF
∠B=∠E
大体こんな感じかな?
問題文のままじゃん!って思ってもこれでOKですよ!
これが書ければ次のステップにいきます。
次は、箇条書きにした条件の間に”なぜそれが成り立つのか”という理由を書いていきます。
今回の問題はは文中に条件が書いてあるので、”問題文でそういう条件だって決めていたよ!”っていうことを書きます。
“問題の中で決まっている条件(出てきた条件)”は「仮定より」という一言で表現できます。
これをさっきの箇条書きに付け加えてみると、
仮定より
AB=DE
BC=EF
∠B=∠E
となります。
証明の答案に近づいてきましたね!
次に合同条件と”合同だよ”という結論を書いていきます。
書いてみると、
仮定より
AB=DE…①
BC=EF…②
∠B=∠E…③
①、②、③より、2組の辺とその間の角がそれぞれ等しいので
△ABC≡△DEF
となります。
ここまで書くといい感じに出来た気がしますね!
ここまで書けたなら満点が欲しい!
しかし、これでは間違いなく減点されてしまいます。
丸をもらうための最後のステップにいきましょう。
次は「仮定より」の前に書き出しの文を入れます。
“今から△ABCと△DEFの関係について書いていくよー”ということが書ければバッチリ!
“問題の指示で△ABCと△DEFが合同だよって証明させられているのにわざわざ今から書くよ!って書かないといけないなんて…”という気持ちはグッと抑えて頑張ってくださいね。
書き出し文をいれてみると
△ABCと△DEFにおいて
仮定より
AB=DE…①
BC=EF…②
∠B=∠E…③
①、②、③より、2組の辺とその間の角がそれぞれ等しいので
△ABC≡△DEF
という感じになります。
これでバッチリ!
「△ABCと△DEFにおいて」というのが、三角形の合同証明をするときのあいさつのようなものだと思ってもらえれば大丈夫です。
こんな感じで書けるようになればいいと思います!
少しずつ、確実に、できるようになっていけばOK!
頑張ってくださいね!
まとめ
今回の記事は”証明の心得”くらいだと思ってるくらいがちょうどいいかなと思います。
丸になるのか、ならないのかということは、最初は分かりにくいです。
“分からないから何も書かない”というのをやめて”とりあえず書く”ことをやってみましょう!
きちんとした日本語で書ければ点はもらえます。
数学っぽい答案はそのうちに書けるようになっていけば大丈夫!
次回は合同条件や証明の書き方などを見ていきます。



