絶対値の中身が文字や二次関数の時の外し方は？

今回は「絶対値って何？外し方ってマイナスがポイント？」の続きになります。

絶対値の中身が正か負で区別を付けて考えましょう。

絶対値の中が正の数のときはそのまま絶対値を消すだけでOK！

一方で絶対値の中身が負の時は-1を掛けて絶対値を外すということでした。

前回は絶対値の中身が数字だけだったのですが、今回はついに文字の入った絶対値の外し方をやっていきます。

苦手な子にはちょっと嫌なところかもしれませんね。

でもここができないと大問1つが壊滅しちゃうという恐ろしいことが起こることがあるので必ずできるようにしておきましょう。

学年的には大体高校1年生で習う内容になります。

絶対値の外し方を理解しよう！

絶対値の外し方はきちんと理屈が分かれば意外と簡単にできます。
ポイントは絶対値の中身が正の数なのか負の数なのかということです。

ここで簡単に復習をしておきましょう。
＜例題＞絶対値をはずそう。

①　\(|+3|\)
②　\(|-3|\)

①は絶対値の中身が正の数なのでそのまま絶対値を外して、\(3\)です。
②は絶対値の中身が負の数です。

絶対値の中身が負の数の時はマイナスの符号を消して絶対値を外しちゃダメですよ！
絶対値の中身が負の数の時は\(-1\)を掛けて外します。

②　\(|-3|=-1 \times (-3)=3\)

よって②の答えは3となります。

絶対値の中身が負の数のときに、マイナスの符号を消して絶対値を外しても同じになりますがこれですると中身が文字になったときに困ってしまうか、文字の入った絶対値を特殊な扱いをすると覚えないと行けなくなるのでオススメしません。

それでは文字の入った絶対値を外してみましょう。

絶対値に文字が入った時の外し方！

＜例題＞絶対値をはずそう。

③　\(|x|\)

絶対値を外す時に意識することは絶対値の中身が正なのか負なのかということでしたね。
\(x\)が正の時と負の時に分けて考えます。
\(0\)は正の時にいれても負の時いれても変わりまらないので、正の方にいれておきます。
\(x \geqq 0\)のとき　（\(x\)が正の数）
絶対値の中身が正なのでそのまま絶対値を外します。
\(|x|=x\)

\(x \leqq 0\) （\(x\)が負の数）
絶対値の中身が負なので\(-1\)を掛けて絶対値を外します。
\(|x|=-1 \times x=-x\)

これでできあがりです。
絶対値の中身が正なのか負なのかを考えればできますね。
このときちょっと考えておきたいのが\(-x\)の符号です。

\(x\)の条件は実数で、今解いた問題は関係なしとします。
\(-x\)は正の数でしょうか？負の数でしょうか？

答えは分かりません！

なぜかというと\(-x\)の\(x\)が正なのか負なのか\(0\)なのかで変わってきます。
ちなみに\(x\)が正のとき\(-x\)は負の数で、\(x\)が負の時\(-x\)は正の数です。
\(x\)が\(0\)のときは\(-x\)は\(0\)ということになります。
数学が苦手な子や\(-x\)のマイナスを見て負の数だと判断してしまう子は、どんなときに正の数になりどんなときに負の数になるのかしっかり分かるようにしておきましょう！

絶対値に二次関数が入った時の外し方！

＜例題＞絶対値をはずそう。

④　\(|x^2-2x-15|\)

絶対値の中に二次関数が入ってきました。

③と比べると少し手間は増えますが基本は変わりません。
絶対値の中身が正なのか負なのかを考えるんでしたね。
二次関数なので見ただけでは分からないのでグラフを書いてみましょう。

こういった場合はとにかくグラフを書くようにしましょう。
グラフを書くことで数式を見ただけでは解けない問題が解けるようになりますよ。
それでは\(y=x^2-2x-15\)グラフを書きます。

今回は\(x^2-2x-15\)が正の数なのか負の数なのかが重要なので\(x\)軸との交点^[1]\(x^2-2x-15\)の解に当たるので\(0=x^2-2x-15\)を求めることで出すことができます。)を出せば良いことになります。

\(y=x^2-2x-15\)
\(y=(x-5)(x+3)\)

となるので、(x,y)=(-3,0),(5,0)で\(x\)軸と交わると言うことになります。

グラフを書くとこんな感じですね！
今回はグラフが正なのか負なのかが大事なので頂点の座標は必要ありませんので出さなくて大丈夫です！

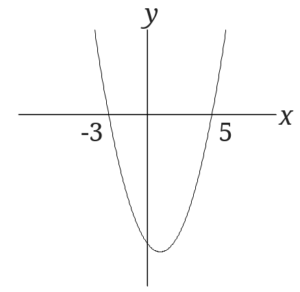
\(x^2-2x-15\)が正になるところと負になるところは分かりますか？
グラフの\(x\)軸の上にある部分は正、グラフの\(x\)軸の下にある部分は負ですよね。

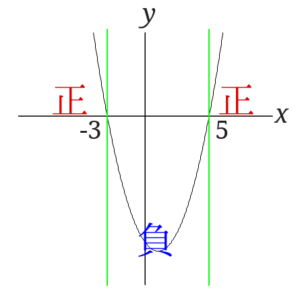
グラフから見ると絶対値の中身は\(x<-3\)、\(x>5\)のとき正で、\(-3 \leqq x \leqq 5\)のとき負となります。
つまり\(x<-3\)、\(x>5\)のときはそのまま絶対値を外し、\(-3 \leqq x \leqq 5\)のときは\(-1\)を掛けて絶対値を外せば良いということになります。

それでは絶対値を外していきますよ。

\(x<-3\)、\(x>5\)のとき
\(|x^2-2x-15|\)
\(=x^2-2x-15\)

\(-3 \leqq x \leqq 5\)のとき
\(|x^2-2x-15|\)
\(=-1 \times (x^2-2x-15)\)
\(=-x^2+2x+15\)

となります。

ポイントは絶対値の中身が正なのか負なのかを考えることと、絶対値の中身が負の時は\(-1\)を掛けて絶対値を外すことです！
ここが分かれば、絶対値を外すことはできるはずです。

まとめ

今回は文字の入った絶対値の外し方でした。
絶対値の外し方は、絶対値の中身が正なのか負なのかがポイントです。
中身が数字であれ文字であれ変わりません。
絶対値が苦手な子はとにかくここが大事です。

絶対値の中に文字が入ったときはその文字の値がどんなときに絶対値の中身が正になるのか、負になるのかが分かれば簡単です。
あとはそのまま絶対値をはずすか\(-1\)を掛けて絶対値を外すかになるのですんなりできると思います。
ただ、二次関数のグラフが書けないと、そもそも絶対値の中身が正のときと負のときの区別ができないので二次関数のグラフは必ず書けるようにしておきましょう！