二等辺三角形と頂角の二等分線の性質を証明！底角は必ず鋭角になるのか？

今回は二等辺三角形の様々な性質やその性質の証明をしていきます。

二等辺三角形とは、2辺の長さが等しい三角形のことです。

証明問題で二等辺三角形を利用するには、まずは二等辺三角形の性質を知ることがその第一歩！

きちんと分からないと証明をするときにどこで二等辺三角形の性質を使えばいいのか分かりませんよね。

今回は二等辺三角形の性質からその証明までしていきます。

二等辺三角形の性質とは？
二等辺三角形の頂角の二等分線
- 二等辺三角形の性質を証明しよう！
二等辺三角形の底角は鋭角？
- 正三角形は二等辺三角形？二等辺三角形は正三角形？
まとめ

二等辺三角形の性質とは？

まずは二等辺三角形の性質を見ていきましょう。

下の図のような\(AB=ACである二等辺三角形ABCがあります。\)
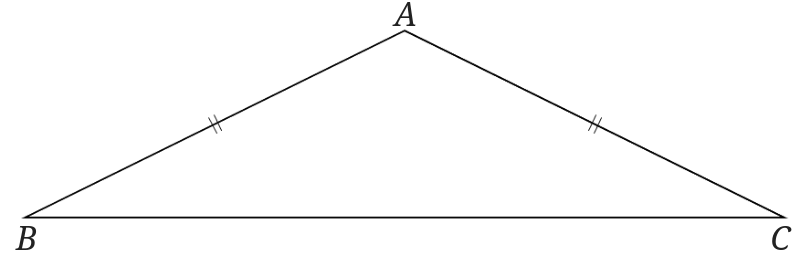二等辺三角形は角に名前がついているのでそこからみていきます。
名前を入れるとこんな感じになります。

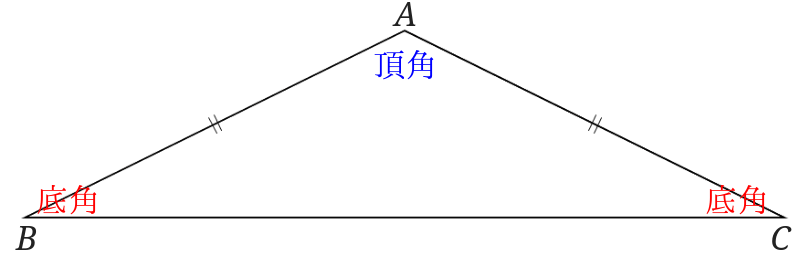
二等辺三角形の等しい2辺からなる角を頂角、頂角の対辺の両端の角を底角といいます。
ここで二等辺三角形の性質を覚えてくださいね。

二等辺三角形の底角は等しい。
これはとっても大事ですよ。

この逆も成り立ちます。
2つの角が等しければその三角形は二等辺三角形であるともいえるんですね！
きちんと覚えてくださいね！！

二等辺三角形の頂角の二等分線

次に下の図のように頂角から対辺に垂線を引きます。
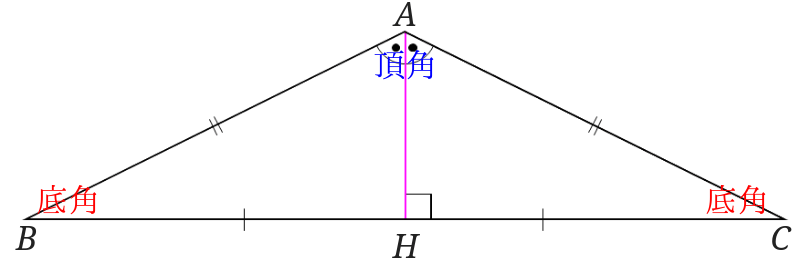すると対辺を二等分にし頂角を二等分していることになります。
見方を変えると頂角の二等分線は対辺と垂直に交わり二等分するとも見えます。
また、頂角と対辺の中点を結ぶと頂角を二等分し対辺と垂直に交わるともいえます。

まずは図ごとしっかり覚えてください。
これはなぜかということを証明してみましょう。
頂角から引いた直線の引き方によって証明が変わってきます。

二等辺三角形の性質を証明しよう！

頂角の二等分線を引いた場合
\(\triangle ABH\)と \(\triangle ACH\)において
\(\triangle ABC\)は二等辺三角形なので\)
\(AB=AC\) ･･･①
\(\angle ABH= \angle ACH\)･･･②
\(AH\)は頂角の二等分線なので、\(\angle BAH= \angle CAH\)･･･③
①,②,③より
1辺とその両端の角がそれぞれ等しいので
\(\triangle ABH \equiv \triangle ACH\)

対辺の中点と頂角を結んだ場合
\(\triangle ABH\)と \(\triangle ACHにおいて\)
\(\triangle ABC\)は二等辺三角形なので
\(AB=AC\) ･･･①
\(\angle ABH= \angle ACH\)･･･②
\(点HはBCの中点なのでBH=CH\)･･･③
①,②,③より
2辺とその間の角がそれぞれ等しいので
\(\triangle ABH \equiv \triangle ACH\)

頂角から対辺に垂線を引いた場合
\(\triangle ABH\)と \(\triangle ACHにおいて\)
\(\triangle ABC\)は二等辺三角形なので
\(AB=AC\) ･･･①
\(\angle ABH= \angle ACH\)･･･②
\(AH\)と\(BC\)は垂直なので\(\angle AHB= \angle AHC=90\)°
①,②,③より
直角三角形の斜辺と1つの鋭角がそれぞれ等しいので
\(\triangle ABH \equiv \triangle ACH\)

頂角から引く線をどのように引くかで少し証明が変わるので注意しておきましょう。

頂角からどのような条件で直線を引く設定なのかを忘れると証明ができないので気を付けてくださいね。

ただどの条件にしてもいっていること自体は変わらないのでそんなにややこしくありません。

上の図をきちんと覚えて、二等辺三角形では底角が等しいこと、頂角の二等分線は対辺を二等分かつ垂直に交わるということを覚えて、さらに証明までできるようにしておきましょう！

それでは二等辺三角形の性質を用いた証明をしてみましょう。

＜例題①＞
下の図のように\(AB=AC\)の二等辺三角形\(\triangle ABC\)があります。
辺\(BC\)を延長し直線BC上に\(BD=CE\)となるように点\(D\)と\(E\)をとります。
このとき\(AD=AE\)であることを証明しましょう。

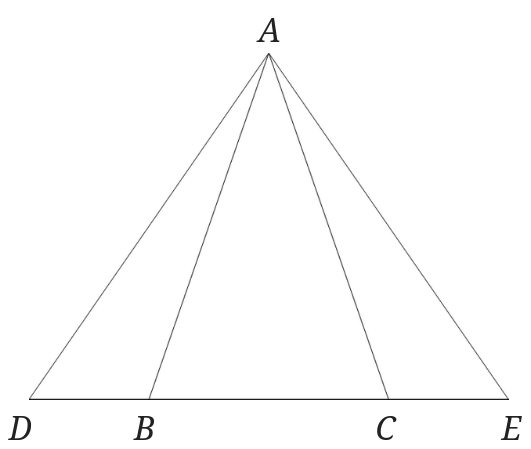
二等辺三角形の性質を使って証明していきましょう。

\(\triangle ADB\)と\(\triangle AEC\)において
\(\triangle ABC\)は二等辺三角形なので
\(AB=AC\)･･･①
仮定より\(BD=CE\)･･･②
\(\angle ABD=180- \angle ABC\)･･･③
\(\angle ACE=180- \angle ACB\)･･･④
二等辺三角形の底角は等しいので
\(\angle ABC= \angle ACB\)･･･⑤
③,④,⑤より
\(\angle ABD= \angle ACE\)･･･⑥
①,②,⑥より
2組の辺とその間の角がそれぞれ等しいので
\(\triangle ADB\equiv \triangle AEC\)
合同な図形の対応する辺は等しいので
\(AD=AE\)

そんなに難しいことはないですね。
今回の証明では「二等辺三角形の底角は等しい」ということを使いました。
ここに気づかないと証明ができません。
二等辺三角形の性質を使うと「長さから形」もしくは「形から長さ」がわかります。

二等辺三角形の底角は鋭角？

たまに聞かれるのが二等辺三角形の底角が鋭角であることの証明。
これは結構すんなりできます。
二等辺三角形の底角は等しいことを利用して証明します。

三角形の内角の和が180°であることを利用します。
頂角\(+2\times \)底角=180
\(2\times\)底角=180-頂角
底角=90-\(\frac{頂角}{2}\)
この時頂角は0°より大きく180°より小さいので、
\(0<\frac{頂角}{2}<90\)となるので
底角\(<90\)となります。

正三角形は二等辺三角形？二等辺三角形は正三角形？

二等辺三角形は、2つの辺が等しい三角形でした。
正三角形は、3つの辺の長さが等しい三角形です。
二等辺三角形は正三角形ではないというのは明らかですよね。^[1]正三角形を二等辺三角形といったときは除きます。

では正三角形は二等辺三角形とみることはできるのでしょうか？
正三角形は3辺の長さが等しい三角形なので当然2つの辺の長さは等しいです。
つまり正三角形は二等辺三角形の条件を備えているので、正三角形は二等辺三角形でもあるということになります。

なのでそれと同時に二等辺三角形の性質ももっているということになります。
そのため頂角の二等分線を頂角から対辺にひくと対辺を垂直に二等分できます。
正三角形はすべての角が\(60\)°なので、どの角からの二等分線でもみんな対辺を垂直に二等分することになります。
二等辺三角形は正三角形とは限りませんが、正三角形は二等辺三角形だと自信をもっていえるようにしておきましょう。