面積が同じ三角形を書くには平行線がとっても便利。
平行線があればいくつでも同じ面積の三角形を書くことができます。
等積変形という名前で中学生で習うはずですが、意外なことに小学生が三角形の面積を習ったときに一応扱われます。算数って侮れませんね。
ただ実際に問題を解くときに使い始めるのは中学3年生くらいからでしょうか。
中学受験を経験した子はきちんと習っているのかもしれませんね。
今回はこの等積変形を扱っていきます。
等積変形は見た目は図形の単元のようにみえると思いますが、実際高校受験では意外と関数でよく使います。
ちょっとした応用問題の中で使うことが多いので解けると周りの子たちに差をつけやすいと思います。
数学が得意な子は是非ともマスターしてください!
それではみていきましょう。
面積が同じ三角形の作り方!
面積が同じ三角形を気軽にたくさん書くことができる書き方をみていきましょう。
下の図のような赤い三角形があります。
直線\(l\)と直線\(m\)の2直線、は平行線です。
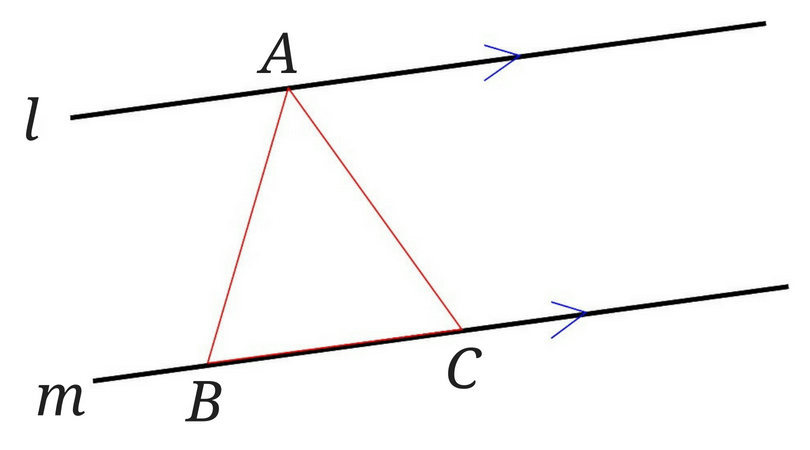
それではこの赤い三角形ABCと面積が等しい三角形を書いていきましょう。
書き方はとっても簡単です。
底辺BCを共有してもう一つの点が直線l上にあれば三角形\(ABC\)と面積が等しい三角形を書くことができます。
それでは1つ書き加えてみますね。
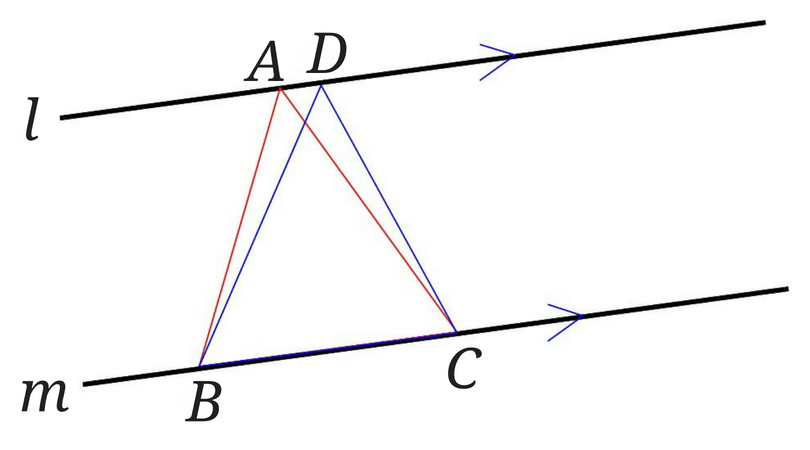
青い三角形\(BCD\)を書き加えてみました。
書き方自体は簡単ですね。
それでは、これらの赤い三角形と青い三角形の面積が等しいこと考えていきましょう!
ここで三角形の面積の公式をみていきましょう!$$(三角形の面積)=(底辺) \times (高さ)\div2$$三角形の面積を出すには底辺と高さがあればよいということになります。
今回書いた赤い三角形と青い三角形は底辺\(BC\)を共有しています。
つまり底辺が等しいということなので、高さが等しければこれらの2つの三角形の面積は等しいといえます。
先ほどの赤い三角形と青い三角形に高さを書き込んでみます。
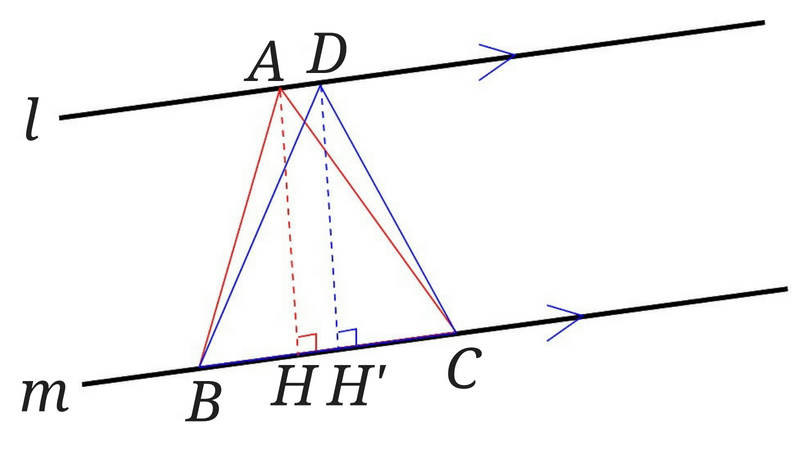
赤い三角形の高さは\(AH\)で、青い三角形の高さは\(DH’\)です。
直線\(l\)と直線\(m\)は平行線なので$$AH=DH’$$となります。
底辺が共通で高さが等しいので、赤い三角形と青い三角形の面積は等しいということが言えます。
また\(BC\)が共通でもう1点を直線\(l\)上にとれば、面積が等しい三角形が作れることになりますよね。
つまり下の図中の三角形はすべて面積が等しいということになります。
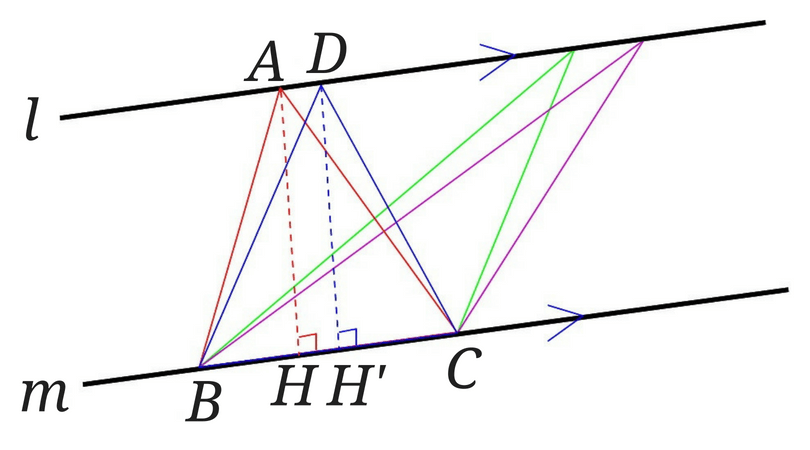
等積変形の問題を解いてみよう!
それでは実際に使ってみましょう!
例題
次の図形の色のついた部分の面積を求めましょう。
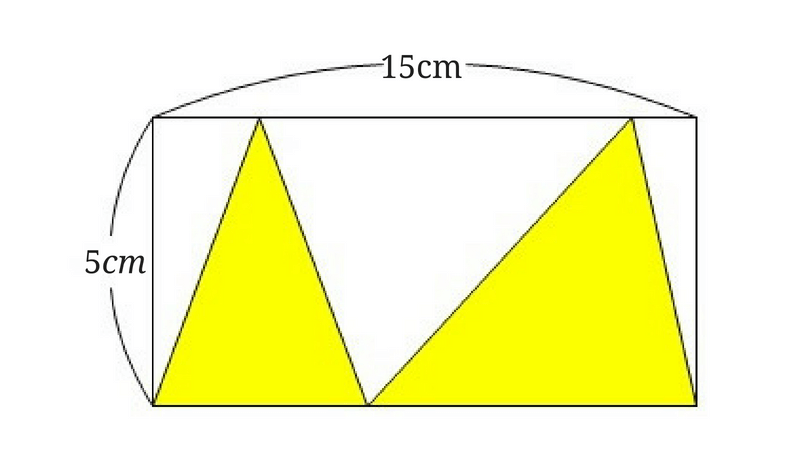
縦の長さが\(5cm\)で横の長さが\(15cm\)の長方形の中に三角形が2つありますね。
2つの三角形の面積の和を求める問題です。
このときに勘違いしたくないのはあくまでも聞かれていることは三角形の面積の和なんですね。
ちなみにこの場合、個々の三角形の面積は求められないんですね。
まずはこの2つの三角形を1つにまとめてみましょう。
この長方形の左端にまとめてみます。
左側の三角形を移動させます。
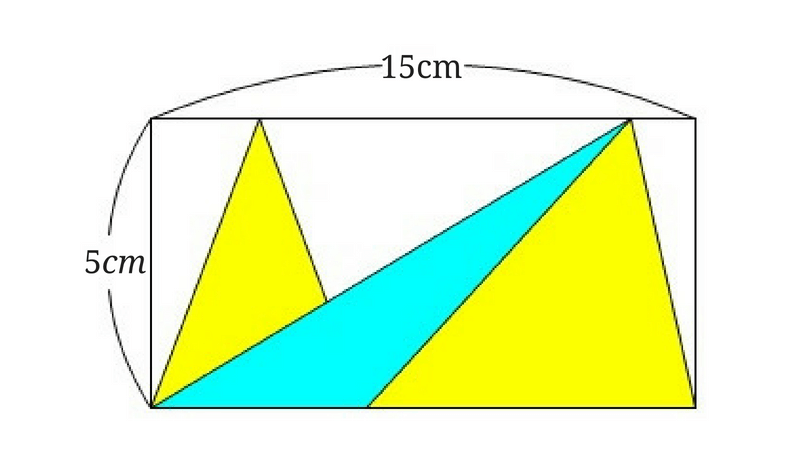
すると下の図のように水色の三角形に変形することができます。
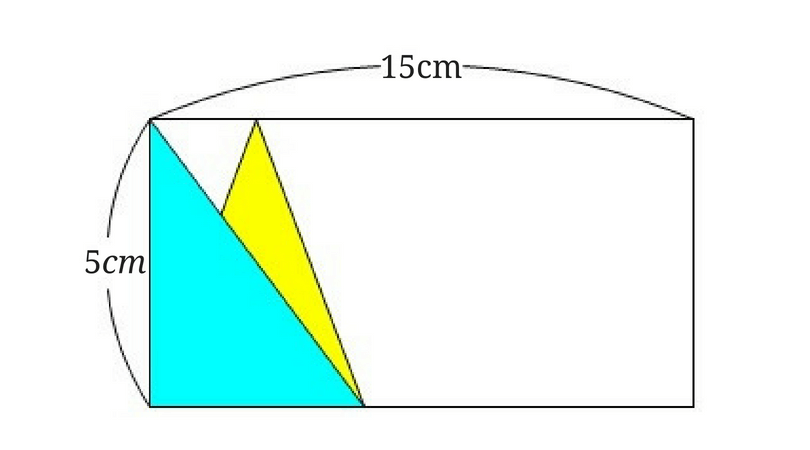
右側の三角形も同じように変形してみましょう。
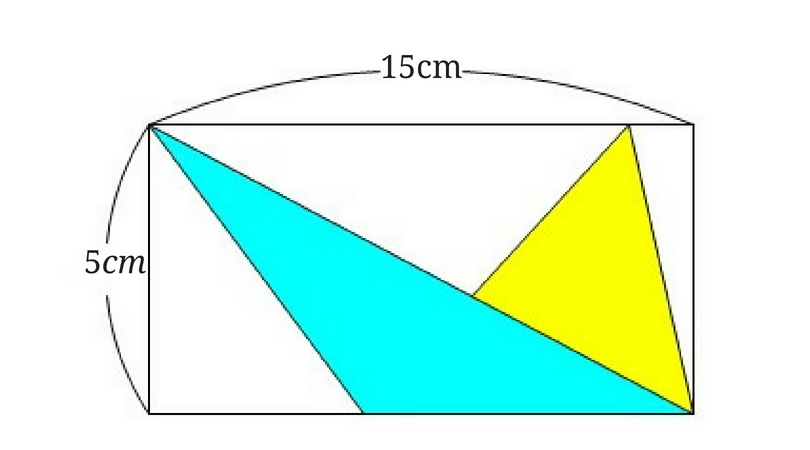
すると2つの黄色い三角形を合わせた面積は下の図のようになります。
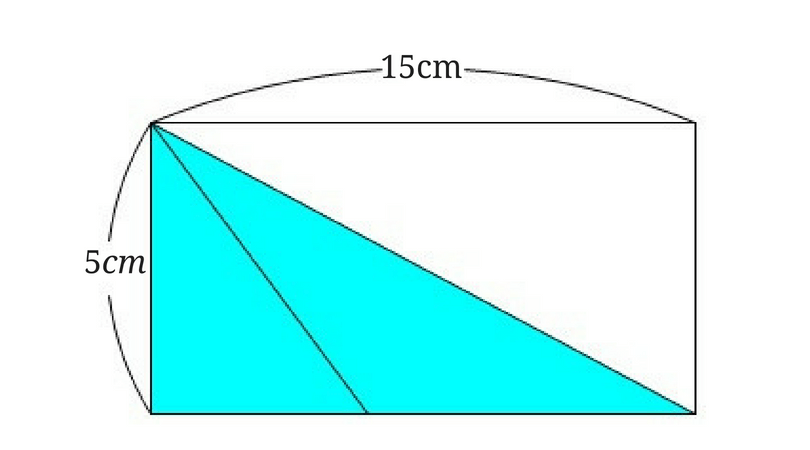
つまり長方形の面積の半分ということになります。$$5 \times 15 \div 2=\frac{75}{2}$$2つの三角形を変形するのが面倒であればこんな感じでも解くことができます。
こちらの方が少し手間が少ないのでほんの少しらくになります。
数学らしく解くなら図のように底辺を文字で置くことでも解くことが可能です。
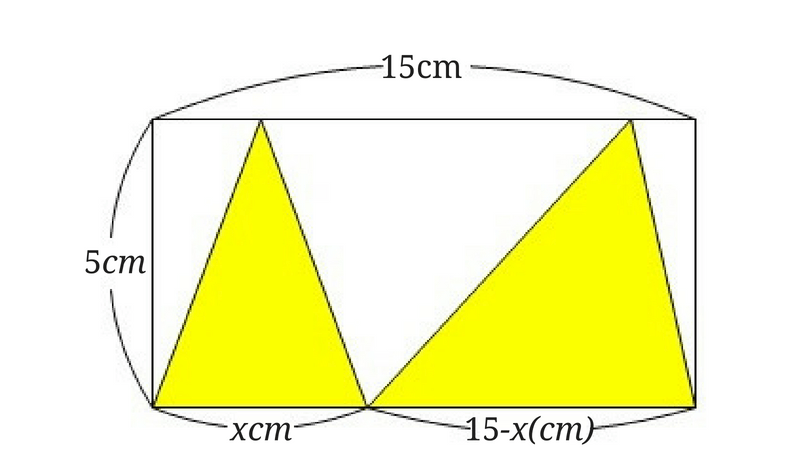
$$5 \times 5x\div2+8 \times (15-x) \div 2=\frac{75}{2}$$左側の三角形の底辺を\(xcm\)とおいたのですが、計算すると\(x\)が消えちゃいましたね。
どの方法でも解くことができますが、同じ面積のまま三角形の形を変えることができる等積変形はマスターしておきましょう。
作図の問題で等積変形を使う場合は等積変形が分からないとお手上げってなってしまいます。
分かるとそんなに難易度が高い作図ないともうので分からないと勿体ないですよ。
作図が出るところだと配点は高いと思うのでしっかり理解してくださいね。
しっかり得点できるようにしましょう!
・等積変形を使って四角形を三角形にしてみよう
まとめ
今回は等積変形についてでした。
平行線をうまく利用すると面積の等しい三角形をたくさん簡単に作ることができます。
理屈自体はそんなにややこしくないので、三角形の面積の公式を絡めてしっかり理解しておくといいと思います。
等積変形を教えてしばらくして、等積変形をして出来た三角形が等しいのかと尋ねて、きちんと答えられる子は意外と少ないです。
実際等積変形を使う上ではこの理屈は特に必要ないのですが図形の面積比を考えたり証明問題を解いたりするときに非常に役に立つと思います。
等積変形を使った三角形をみて瞬時になぜその2つの三角形が等しいのか理解できるとばっちりです。
平行線が真横だと見て理解しやすいのですが平行線が斜めだと分かりにくくなり、面積が等しいことなどに気づきにくくなるので注意が必要です。
たとえ平行線が斜めでもきちんと見て気づけるようにしておきましょう。




