数学の図形で使えるスリッパの法則を使って星の角度の和をだそう！

前回の記事「三角形の内角の和が180度である理由は？外角の和や多角形の公式を導こう！」では多角形の内角の和や外角の和について考えてみました。

\(n\)角形の内角の和\(=180(n-2)°\)
\(n\)角形の外角の和\(=360°\)
でしたね！

これらは平面図形の基本になるのできちんと覚えておきましょう。

ちゃんと理由まで覚えておけばばっちりです。

今回はスリッパの法則なんて呼ばれることもある公式をみていきます。

この公式は知らなくても、一応問題は解くことができますが、スリッパの法則を覚えずに解くのはかなり難しいと思われる問題があるので覚えておいていたほうがいい公式の1つになります。

覚えておくとただ計算が速くなるというだけではなく、問題を解きやすくなる便利な公式です。

公式を丸暗記するのもいいのですがきちんと別の方向から見ていくと三角形の内角の和の理解が深まるのでそちらからみていきたいと思います。

この記事では、数学の図形で使えるスリッパの法則や星の角度の和について書いてみたいと思います。

数学の図形で使えるスリッパの法則って！？

三角形の内角の和は180°です。
このことの証明ってできますか？
三角形の内角の和の証明がスリッパの法則の元になります。
それでは、三角形の内角の和が180°である証明をします。

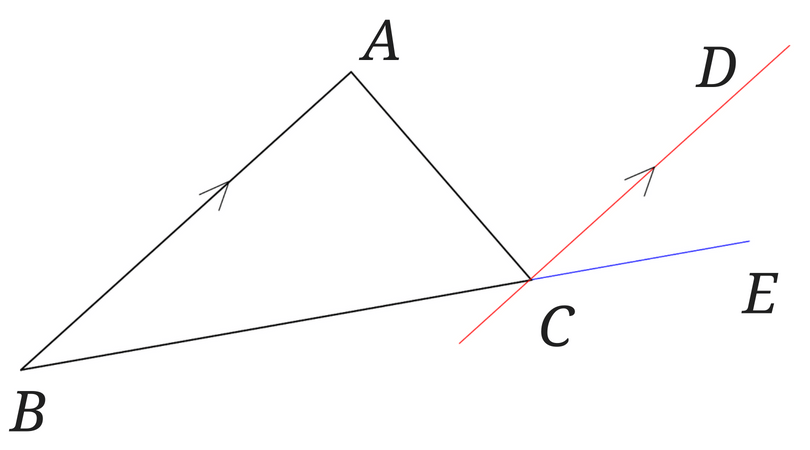
△ABCがあるところに、辺\(BC\)を延長し（青線）、辺\(AB\)に平行で点\(C\)を通る直線(赤線)をひいたところです。
それでは三角形の内角の和が\(180°\)であることを証明していきますね。

\(AB∥CD\)より
平行線の同位角が等しいので、\(∠ABC=∠DCE\)
平行線の錯角が等しいので、\(∠BAC=∠ACD\)

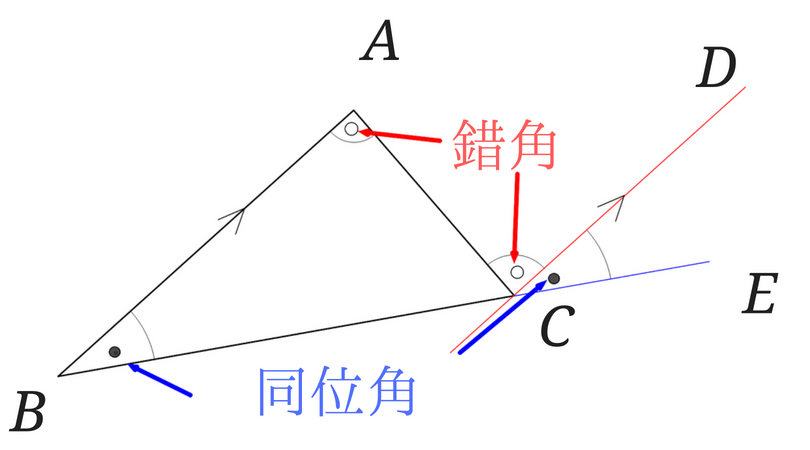
よって三角形の内角の和は\(180°\)ということになるのですが、少し見方を変えてみましょう。
いっていることは、ほとんど変わらないのできちんと理解できるようにするといいと思います。
図がごちゃごちゃしているのでちょっと図をすっきりさせます。

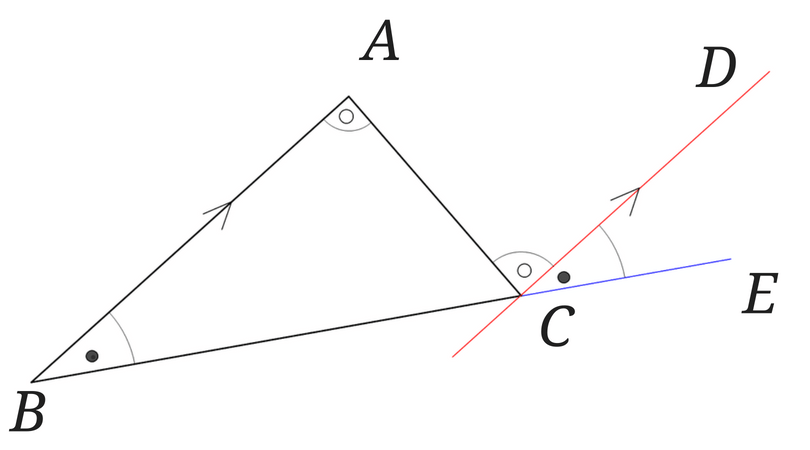
この図から
\(∠BAC=∠ACD\)
\(∠ABC=∠DCE\)
ですよね。

つまりこの二つの式から分かることは、
\(∠BAC+∠ABC=∠ACD+∠DCE\)
\(∠ACE=∠ACD+∠DCE\)
よって
\(∠BAC+∠ABC=∠ACE\)となります。

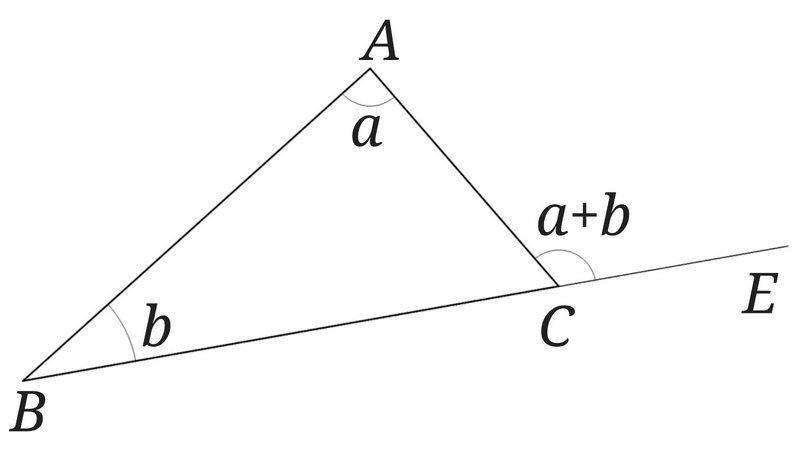
図で示すとこんな感じですね。
三角形の2つの内角の和はその2つの内角のどちらともとなり合わない外角に等しいということです。
言葉で覚えても分かりにくいので、図のようなイメージで覚えられるといいと思います。
記号ではなく角同士の位置関係で図形の中で見たら分かるという形で覚えておくと使いやすい公式の1つになります。

誰が言い出したのかは知りませんが、この公式にはニックネームがあって、「スリッパの法則」って呼ばれています。
スリッパに似ているからですかね？？笑
なんだ難しい公式じゃないじゃん！と思うかもしれませんが、これは覚えておかないと解きにくい問題に出会うことがあるので覚えておきたいところです！

星の角度の和を求めよう！

星の角度の和を求めようといっても別に天体と関係ありません。
下に星の形をした図形があります。
印がつけてある角の和を求めてみましょう。

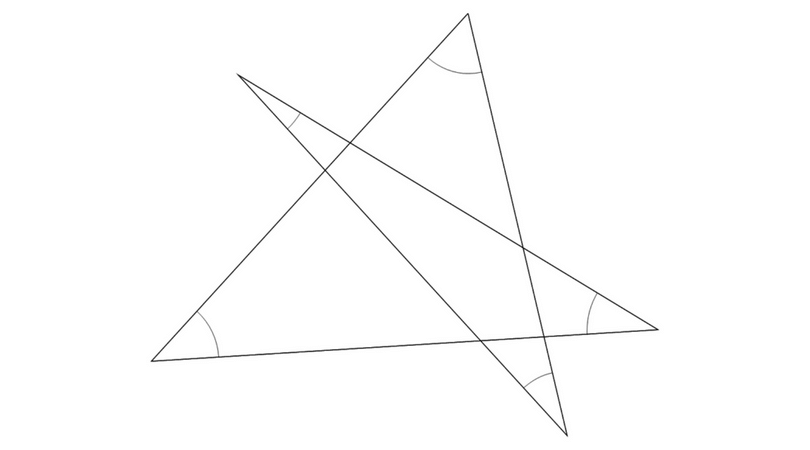
星の先っぽに印が書いてありますね！
これらの5つの和を求める問題です。
数字が1つもありません。

ここで勘違いしてはいけないのは、あくまでも5つの角の和を求めるということです！
1つ1つの角の大きさは聞かれていません。
1つ1つの角を求めようとする子がたまにいますがそれは無理です！

それでは5つの角の和について考えていきます。

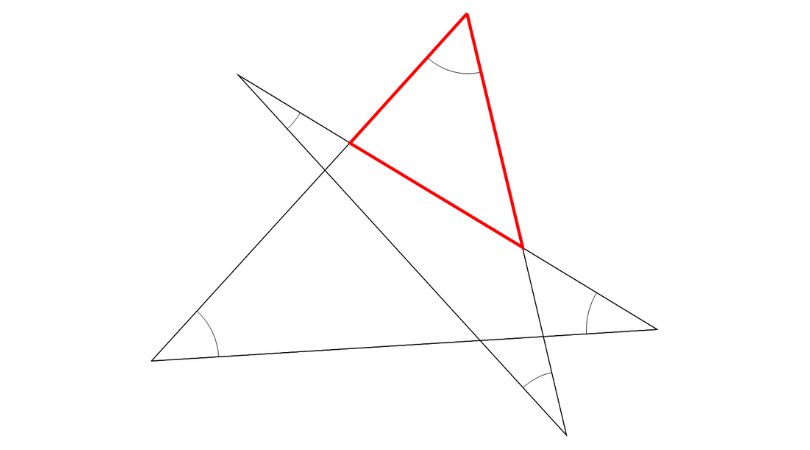
図の中に赤い三角形を書き込んでみました。
この赤い三角形に散り散りになっている5つの角全部を集めていきたいと思います。

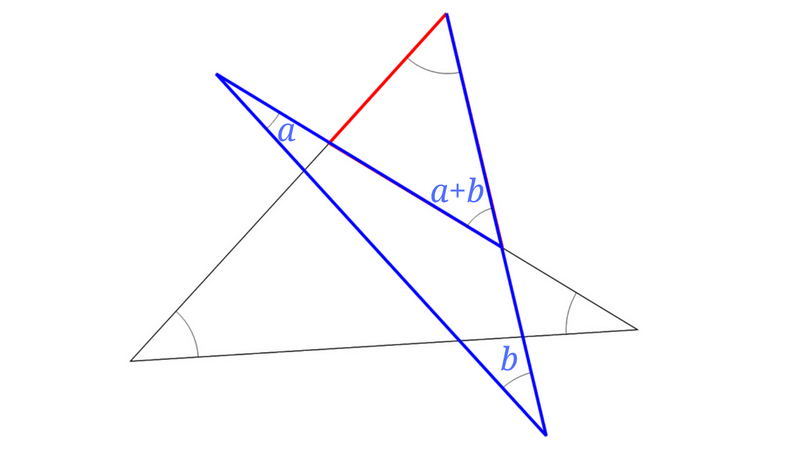
図の中に青い線も書き込んでみました。

この三角形と1つの外角でみていくと、
青い三角形の印のついた2つの内角の和は隣り合っていない外角と等しくなります。
スリッパの法則ですね！

今度は図の中に緑の線を書き込んでみました。

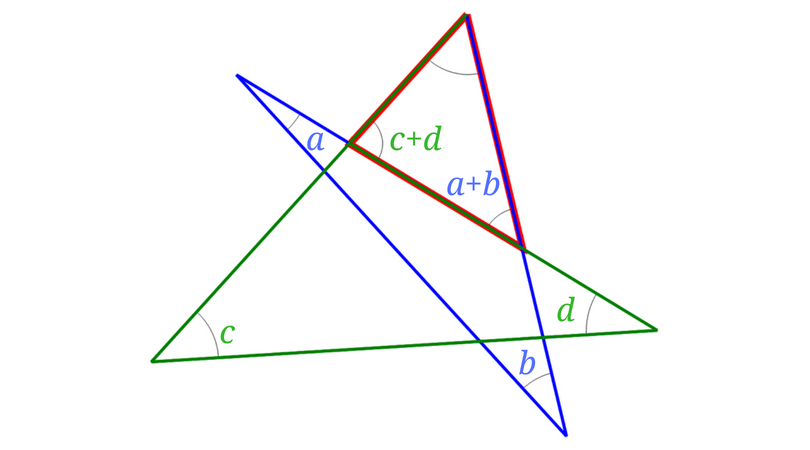
さっきと同じようにスリッパの法則を使って、緑の三角形の印のついた2つの内角の和は隣り合っていない外角と等しくなります。
これで星の先っぽの5カ所に散らばっていた角が、赤の三角形の内角に移動することができました。
つまり星の先っぽの5カ所の角の合計は180°ということになります。
1つ1つの角は求められませんが、5つの角の和であれば求めることができましたね！

図形の角度の和も求めよう！

もう一題やってみましょう！

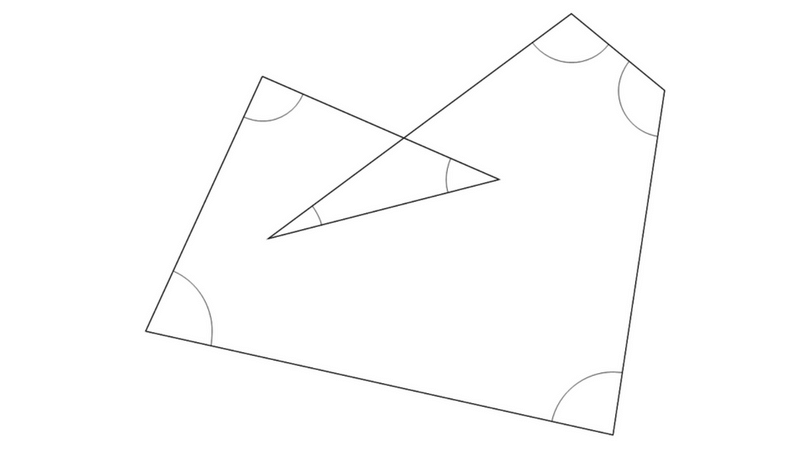
今度は星形ではない形にしてみました。
これもよく見かける問題ですね。
印のつけてある角の和を求めてみましょう。

中に三角形があるのでそこでスリッパの法則を使ってみてくださいね。
まずは自分で考えてみましょう。
解けなくてもまずは何か書き込んでみたり、考えてみたりすればOK！

そうしているうちに解き方がなんとなく分かってくることがあるかもしれませんよ。

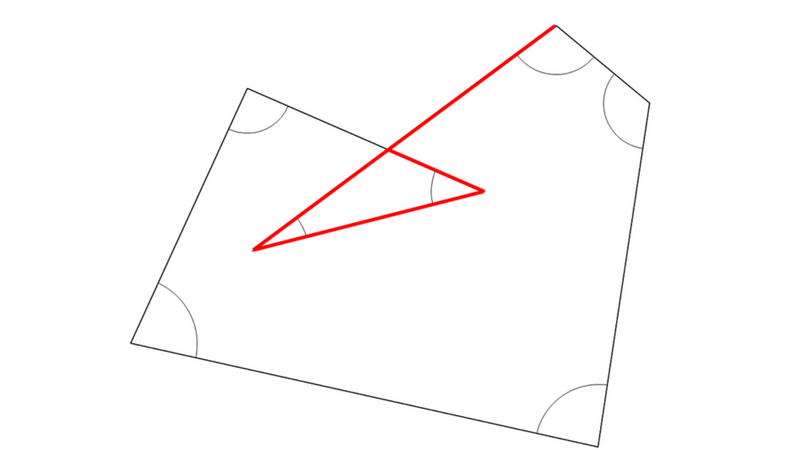
図の赤線のところでスリッパの法則を使ってみましょう。
すると三角形の内角にある2つの三角形を外角にもっていくことができます。
また青線の形でみると、この形は六角形です。

内角の和を求めると
180(6-2)=720°^[1] \(n\)角形の内角の和\(=180(n-2)\)で求めることができます。
になります。

で、この図形を眺めてみると六角形の内角で一部だけ欠けているのがわかりますか？

つまり六角形の内角の和からこの欠けている部分をひけば答えがだせますね。
この欠けている部分は直線なので180°です。

六角形の内角の和から180°をひいて、
\(720°-180°=540°\)
になります。

まとめ

今回の記事では、数学の図形で使えるスリッパの法則や星の角度の和について書いてみました。
スリッパの法則は、三角形の内角の和から考えれば当たり前の内容なのかもしれません。
しかし、図形の問題を解くうえでスリッパの法則を知らずに解くのは難しいのではないでしょうか。
星の角の和を求めるような問題を解く時にはすごく力を発揮してくれます。
知らなければ気づくのが難しいのではないでしょうか？
図形の問題では気づかなければ手も足もでませんからね･･･

単に言葉で覚えるだけではあまり使えない公式なので、しっかり図形の中で暗記してスリッパの法則を使えるようにしておきましょう。
スリッパの法則で大切なのは位置関係ですよ。