等積変形でよく出てくる作図の説明です。
学校の数学のワークでもよく見かけます。
実際はそんなに難しいものではないと思うのですが、ちょっと理屈がめんどくさそうということで流しちゃう子も結構見かけます。
それでは作図をしていきましょう。
等積変形の作図
等積変形の作図をするにはきちんと基本的な作図の仕方を押さえておくことが大事です。
きちんと理解して覚えていますか?
もし「等積変形ってなに?」みたいな状態であればまずは等積変形を理解してきてくださいね。
・等積変形を使った面積が同じ三角形の書き方
それでは初めによく見かける等積変形の問題を扱ってみますね。
等積変形を使って四角形を三角形に作図する方法
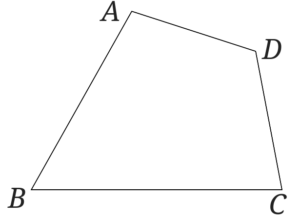
右の図のような四角形があります。
この四角形を直線\(BC\)の\(C\)の右側に点\(P\)をとり四角形\(ABCD=\triangle ABP\)となるような点\(P\)を作図しましょう。
中学校でよく使う数学のワークでよく見かける問題だと思います。
中間考査や期末考査のような定期考査ではよく見かける問題ですね。
それでは作図していきましょう。
まずは辺\(BC\)を\(C\)の方に延長します。
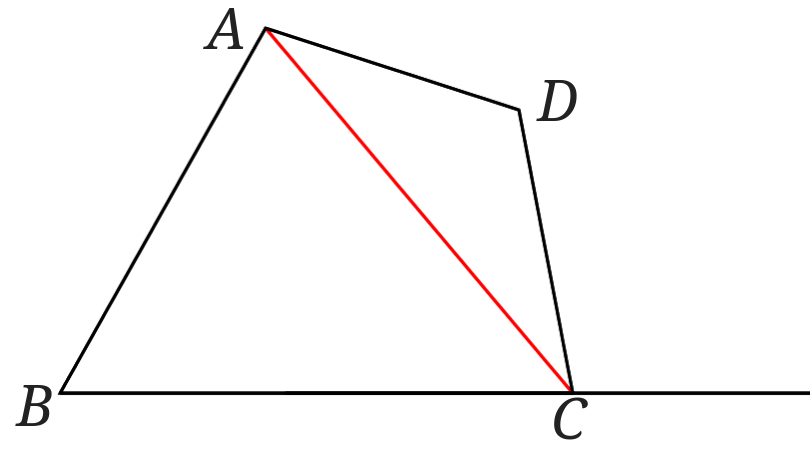
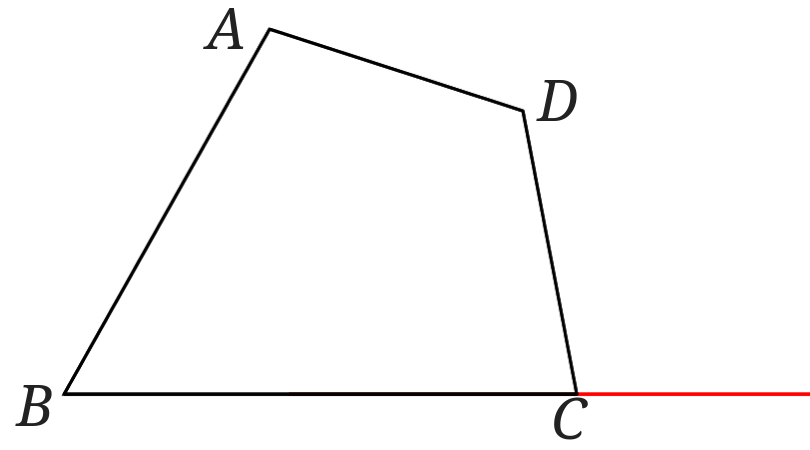 \(A\)と\(C\)を結んで直線\(AC\)を引きます。
\(A\)と\(C\)を結んで直線\(AC\)を引きます。
 次に直線\(AC\)に平行で点\(D\)を通る直線を引きます
次に直線\(AC\)に平行で点\(D\)を通る直線を引きます
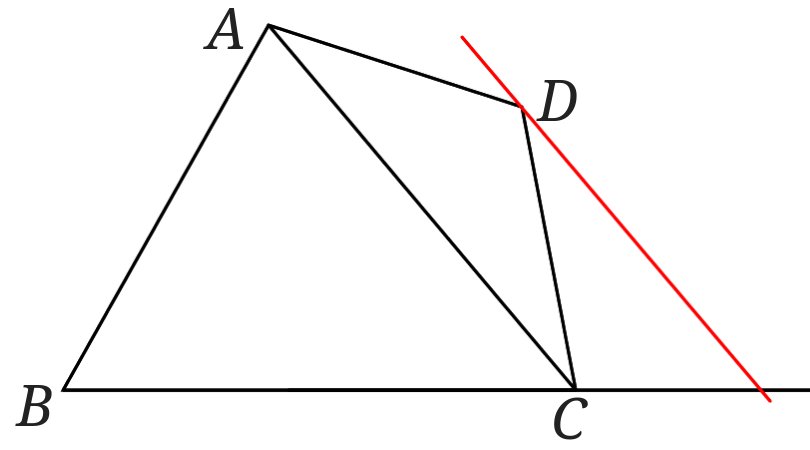
点\(D\)を通る直線\(AC\)に平行な直線と直線\(BC\)との交点が求める点\(P\)になります。
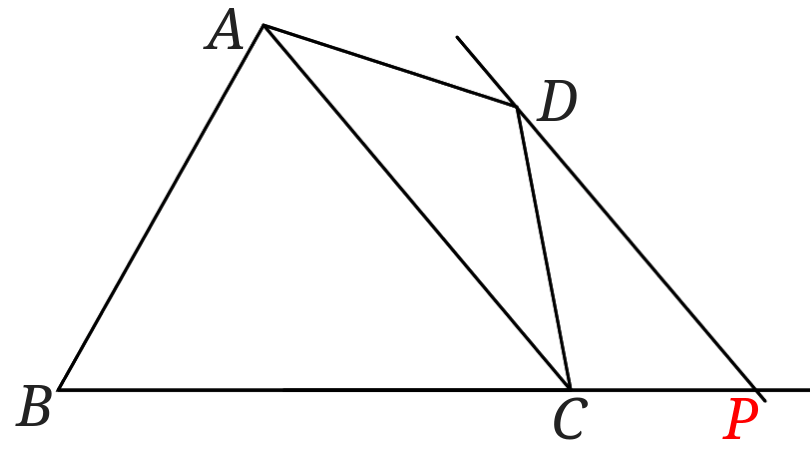 点\(P\)と点\(A\)を結ぶと四角形\(ABCD=\triangle ABP\)となる点\(P\)が作図できたことになります。
点\(P\)と点\(A\)を結ぶと四角形\(ABCD=\triangle ABP\)となる点\(P\)が作図できたことになります。
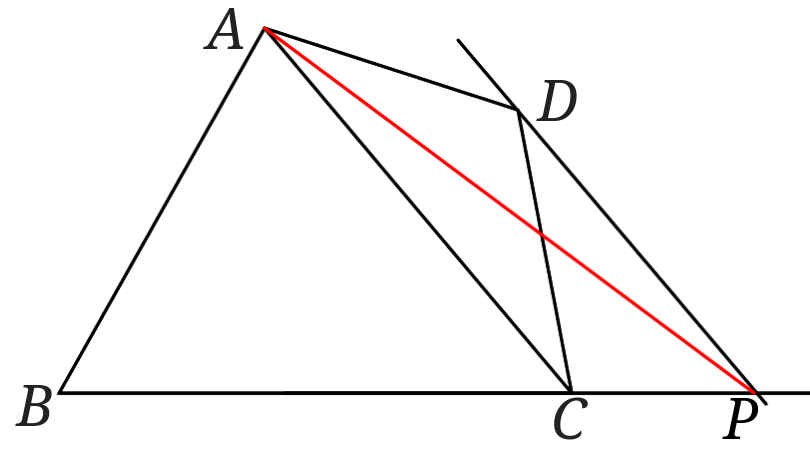 これが等積変形を使った四角形を三角形にするやり方なのですが、これで\(ABCD=\triangle ABP\)が成り立っていることは理解できますか?
これが等積変形を使った四角形を三角形にするやり方なのですが、これで\(ABCD=\triangle ABP\)が成り立っていることは理解できますか?
このやり方を覚えることはそんなに難しくないと思いますが、これが等しいということを説明していきますね。
まずは先ほどの四角形から見ていきましょう。
四角形を二つの三角形に分けます。
 赤い三角形の\(\triangle ABC\)と黄色い三角形の\(\triangle ACD\)に分けてみました。
赤い三角形の\(\triangle ABC\)と黄色い三角形の\(\triangle ACD\)に分けてみました。
次に作図した\(\triangle ABP\)を2つの三角形に分けます。
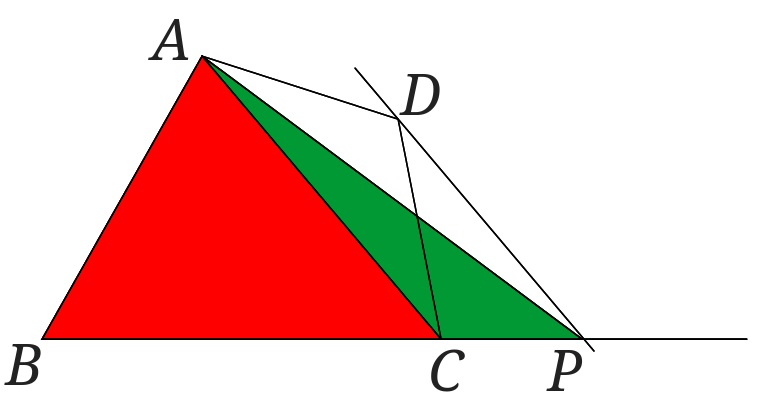 それぞれ2つの三角形に分けてみました。
それぞれ2つの三角形に分けてみました。
分かりやすくするために2つ並べてみます。
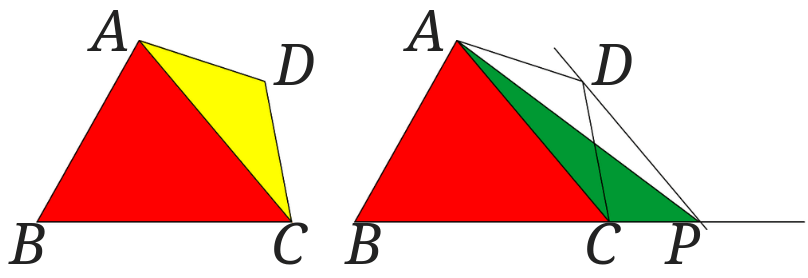 この図を見てみると、赤い三角形の部分は面積が等しいですよね。
この図を見てみると、赤い三角形の部分は面積が等しいですよね。
ということは黄色の三角形と緑の三角形の面積が等しければ、元の四角形\(ABCD\)と\(\triangle ABP\)の面積が等しいということが言えます。
黄色の三角形と緑の三角形は\(AC\)を底辺とみます。
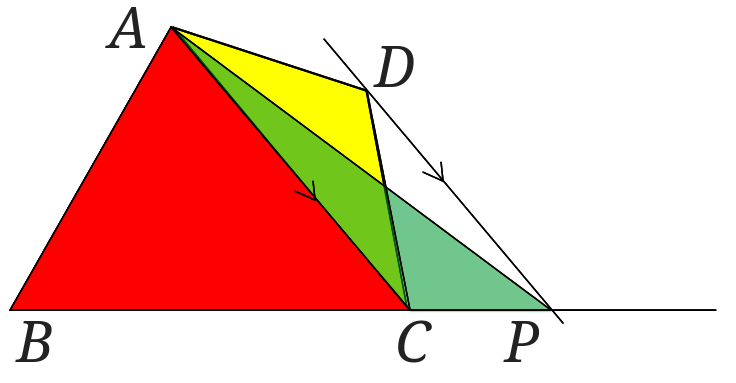 すると\(AC//DP\)なので、2つの三角形の面積は等しいということになります。
すると\(AC//DP\)なので、2つの三角形の面積は等しいということになります。
と、いうわけで、四角形\(ABCD=\triangle ABP\)が成り立つと言えます。
面積をそのままで四角形を三角形にする作図ができました。
作図の仕方を丸暗記するんじゃなくてしっかり理解してくださいね。
等積変形を使って二等分線を書く
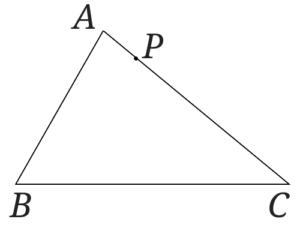
右のような三角形があります。
点\(P\)を通る\(\triangle ABC\)の面積を二等分する直線を書きましょう。
この問題は、二次関数のなかで三角形の面積を二等分するときに使うことができます。
作図の仕方を思いつくのが難しいかもしれません。
二通りの作図をしてみますね。
三角形の二等分線の作図1
まずは点\(P\)と点\(B\)を結びます。
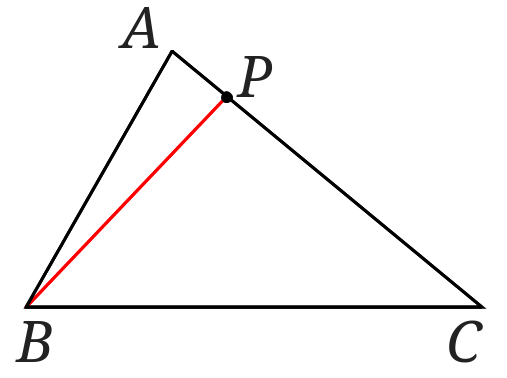
次に点\(A\)を通り直線\(BP\)に平行な直線を引きます。
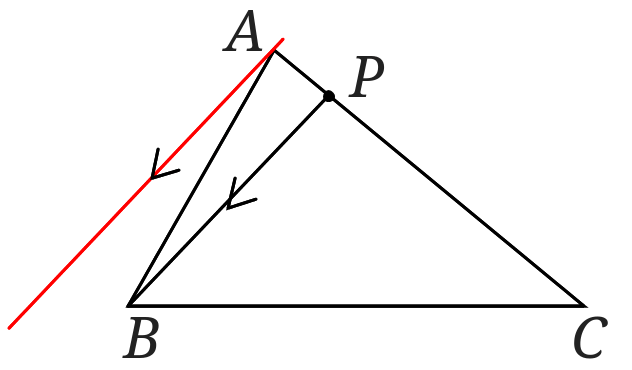
直線\(BC\)を\(B\)の方に延長し、直線\(BC\)と点\(A\)を通り直線\(BP\)に平行な直線との交点を\(R\)とします。
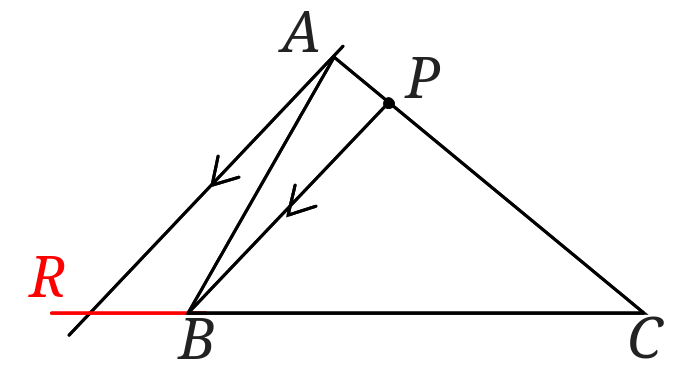
点\(P\)と点\(R\)を結びます。
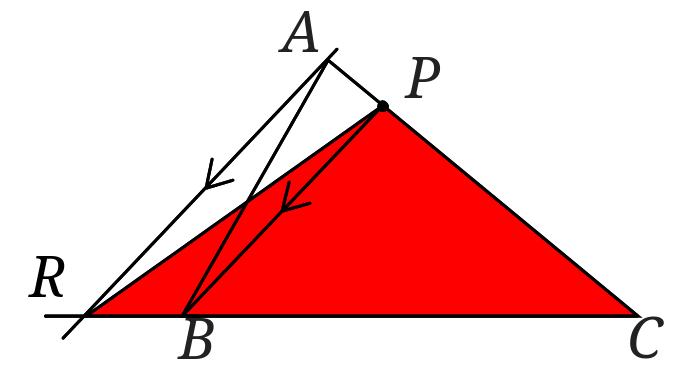
\(AR//PB\)なので\(\triangle ABC=\triangle PRC\)となります。
次に\(\triangle RPC\)を中心にみていきます。
\(RC\)の中点を\(M\)[1]垂直二等分線を引いて中点を取ってくださいね。定規ではかっちゃダメですよ。として点\(P\)と点\(M\)を結びます。まずは線分\(RC\)の垂直二等分線を書きます。
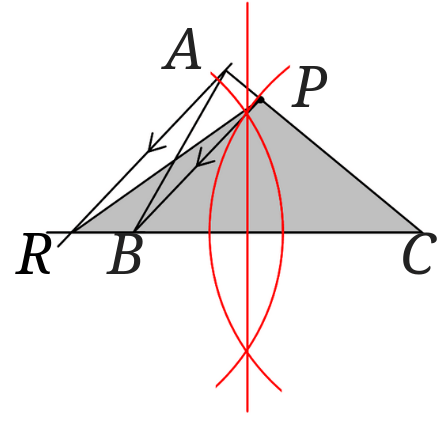
あとは線分\(RC\)の垂直二等分線と線分RCの交点を結びます。
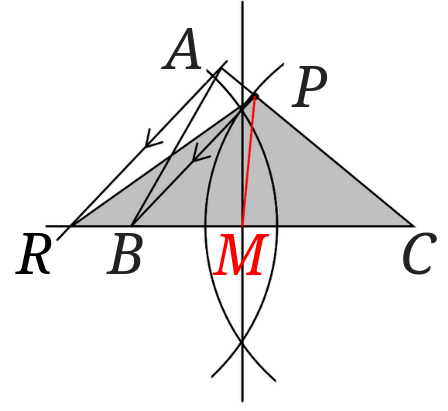
これで点\(P\)を通り\(\triangle ABC\)を二等分する直線\(PM\)を書くことができました。
三角形の二等分線の作図2
ちょっと違う方法でやってみたいと思います。
点\(B\)と\(AC\)の中点\(M\)[2]垂直二等分線を引いて中点を取ってくださいね。定規ではかっちゃダメですよ。を結び、点\(P\)と\(B\)を結び、さらに点\(M\)を通り直線\(PB\)に平行な直線を引き、直線\(BC\)との交点を\(N\)とします。
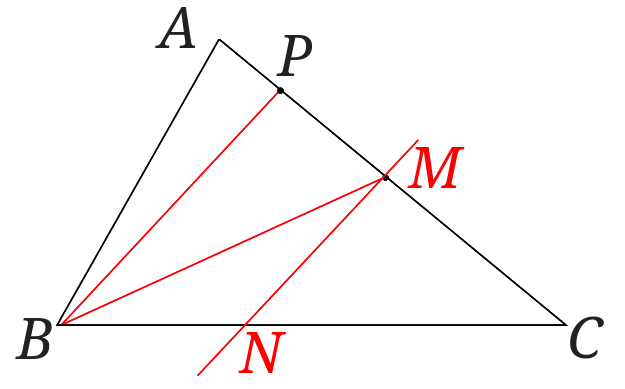
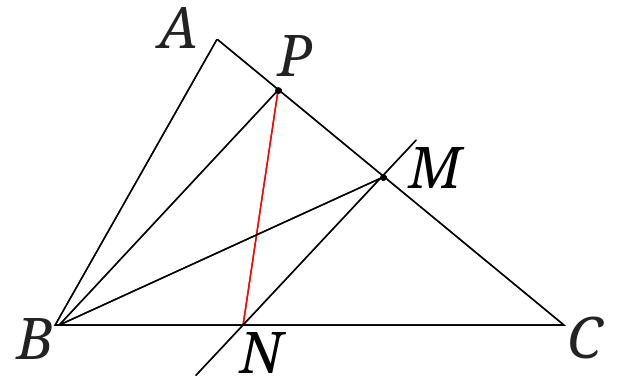
あとは点\(P\)と点\(N\)を結んでできあがりです。
まとめ
今回は等積変形でよく出てくる作図を2つ扱いました。
1つ目の四角形を同じ面積の三角形に等積変形を利用しての作図は特によく出るので必ずマスターしておきましょう。
中間考査や期末考査でも頻出の内容になります。
2つ目にした三角形の二等分の仕方はちょっと難しいかもしれません。
二次関数のなかで三角形の二等分線を出すときに使うことがあります。
知らなくても根性で何とかできることがほとんどだと思いますので、こちらの作図はできなくても1つ目の作図はできるようにしておいてくださいね!
もちろんどちらも出来るのが1番いいですよ。




