4つの乗法公式の使い方と覚える必要性の有無

今回は乗法公式をの使い方をしていきます。

公立中学で習うのは中学3年生のはじめくらいになります。

乗法公式というくらいなので一応公式なのですが、困ったことに丸暗記をしてもなかなか使いにくい公式です。

一応公式は中間考査や期末考査のような定期考査を見据えて書けるようにはした方がいいのですが、覚えてヨロヨロしながら頑張って使いながら展開するくらいなら諦めて分配法則で全部展開してしまった方が早いです！笑

ただそれでは展開公式の扱いに慣れることができないので今回は乗法公式をどのようにみて展開すればいいかについて書いていきます。

乗法公式を4つ覚えよう！

まずは4つの乗法公式を覚えましょう！

$$(x+a)(x+b)=x^2+(a+b)x+ab$$

$$(a+b)^2=a^2+2ab+b^2$$

$$(a-b)^2=a^2-2ab+b^2$$

$$(a+b)(a-b)=a^2-b^2$$

覚えましょうしょうと言ってもこれが覚えてもなかなか使いにくいですよね。
まじめな子ほど一生懸命公式に代入して頑張るのですが、これがまた難しいこと…

覚えるだけでは使いにくいのでしっかり乗法公式の使い方をマスターしましょう。

乗法公式の使い方

\( (x+a)(x+b)=x^2+(a+b)x+ab\)を使った式の展開

まずは公式をそのまま使った式の展開のやり方を見ていきましょう。

＜例題＞
次の式を展開しましょう。
①\( (x+3)(x-5)\)
\( (x+a)(x+b)=x^2+(a+b)x+ab\)が使えそうですね。
この乗法公式と比較すると、\(a=3\)、\(b=-5\)になります。
乗法公式の右辺に代入すると、
\(x^2+(3-5)x+3\times (-5)\)
\(=x^2-2x-15\)
これで出来上がりなんですが、結構やりにくいですよね。
式に書いてしまうと伝わりにくいのですが、自身で公式に代入しながらしてみてください。
なかなか難しいですよ。

それではどのように公式を扱っていけばいいのでしょうか。

実際に公式を使って展開するときには公式に代入するというよりも場所を見ながらした方がいいですね！

それでは先ほどの\( (x+3)(x-5)\)を展開してみましょう。
初めの\(x^2\)は大丈夫ですね！
次は\(x\)の係数を出します。

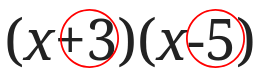
\(x\)の係数はまるで囲んだところの和です。
つまり\(x\)の係数は\(+3+(-5)\)になります。
よって\(x\)の係数は\(-2\)ですね。

次に最後の定数項は丸で囲んだ数の積になります。
つまり\(+3\times (-5)=-15\)となり、
\( (x+3)(x-5)\)を展開すると\(=x^2-2x-15\)
となります。

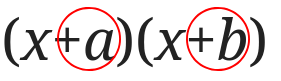
\( (x+a)(x+b)\)を展開するには、 \(x\)の係数は赤い○のついたところの和、定数項は赤い○のついたところの積になると覚えましょう。
公式で覚えるとなかなか使いにくいのが、どこの項の和なのか、積なのかを場所を基準に考えるだけでぐっと使いやすい公式に早変わりします。

乗法公式の、$$(a+b)^2=a^2+2ab+b^2$$も同じように式の場所に着目するとかなり使いやすい公式になります。

\( (a+b)^2=a^2+2ab+b^2\)を使った式の展開

この公式も先ほどの公式と同じでそのまま使うとめんどくさいです。
下の図のような感じで、\(a\)を前\(b\)を後ろとみます。

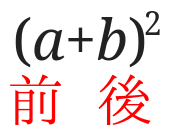
2乗の公式は、「前2乗2倍の前後ろ後ろの2乗」って感じですると上手くいきます。
それでは実際にやってみましょう。

＜例題＞
\( (x+3)^2\)の展開をしてみましょう。

前2乗なので\(x^2\)
次に2倍の前後ろなので、\(2\times x\times 3=6x\)
最後に後ろ2乗なので\(3^2=9\)となり
答えは\(x^2+6x+9\)となります。

「前2乗2倍の前後ろ後ろの2乗」という言葉は覚えなくても大丈夫ですよ。
場所で覚えてもらえれば大丈夫です。
頭で考えるときはココを2乗して･･･くらいに考えてくれればいけますよ。

ここで\( (a+b)^2=a^2+2ab+b^2\)と似た^[1]\( (a+b)^2=a^2+2ab+b^2\)に\(b=-b\)を代入すれば\( (a-b)^2=a^2-2ab+b^2\)は簡単に導くことができます。普通に分配法則で展開しても同じ結果になります。乗法公式がありましたよね。
\((a+b)^2=a^2+2ab+b^2\)と\( (a-b)^2=a^2-2ab+b^2\)とはほとんど同じ公式です。

\( (a-b)^2=a^2-2ab+b^2\)をの公式を使う際は間の項の符号をマイナスにするだけで\( (a+b)^2=a^2+2ab+b^2\)の公式と使い方は同じです。

最後に\( (a+b)(a-b)=a^2-b^2\)の展開ですね。
これは簡単ですね。
まずは前の括弧のなかと後ろの括弧の中身が符号が1つ違えば使える公式です。

\( (a+b)(a-b)=a^2-b^2\)を使った式の展開

\( (a+b)(a-b)=a^2-b^2\)の公式を使える場合の特徴を覚えましょう。

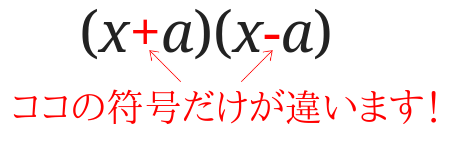
\( (a+b)(a-b)=a^2-b^2\)が使えると判断できたら実際に展開するには赤○の2乗マイナス青○の2乗と覚えれば大丈夫です。

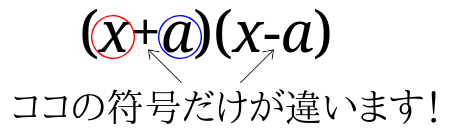
この公式も、どこを2乗するのかが分かれば大丈夫です。

それでは実際にやってみましょう。

＜例題＞
\( (x+3)(x-3)\)の展開をしてみましょう。

括弧の中身が３についた符号が違うだけであとは同じです。
そこに気づくことが出来れば、\( (a+b)(a-b)=a^2-b^2\)を使って展開するだけです。

\( (a+b)(a-b)=a^2-b^2\)を使って展開する際は最初の括弧の中身だけ見ていれば大丈夫です。
つまり\(x+3\)となっているので、\(x^2-3^2=x^2-9\)となります。

括弧の中の、前の項の2乗マイナス後ろの項の2乗と覚えておけば大丈夫です。

乗法公式は覚える必要があるのか？

特に覚えなくても大丈夫な気がしますが、その後に習う因数分解を考えると頭にある程度入れておく方がいいのではないでしょうか。
因数分解の単元でしっかり覚えれば何とかなります。
乗法公式を使わなくても展開はできますので、試験中がに公式に自信がない場合は、分配法則のみでゴリゴリ解いても問題ありません。
まずはきちんと展開ができるようになってから公式は書けるようにすればいいのではないでしょうか。

まとめ

今回は乗法公式についてでした。

乗法公式は覚えるべきか否か迷うところではあります。

覚えたところですごく役に立つ公式でもないので、因数分解が終わるまでに一通り公式が書けるようになっていればいいと思います。

公式にとりつかれたように暗記して全く使えない知識を増やしても仕方がありませんからね。

まずは正確に式を展開できるようになることを目標に学習していきましょう。