中学3年生の乗法公式が終わるといよいよ因数分解です。
今まで2×3を解いて6という感じの計算ばかりでしたが、因数分解では6を2×3のようにすることをいいます。
形だけ見ると素因数分解みたいですね。
素因数分解では数字のみを扱うのですが因数分解では文字が入ってくるので見た目には難しくなります。
目次
中学で習う因数分解の公式は？
まずは公式を見ていきましょう。
中学生で習う公式を挙げてみます。
$$ax+bx+cx=x(a+b+c)$$$$x^2+(a+b)x+ab=(x+a)(x+b)$$$$a^2+2ab+b^2=(a+b)^2$$$$a^2-b^2=(a+b)(a-b)$$
それでは実際に因数分解をしてみましょう。
因数分解の公式の使い方を解説
$$ax+bx+cx=x(a+b+c)$$
1番はじめの公式はちょっと無理矢理作ってみました。
共通因数でくくるって言われる公式(？)です。
それぞれの項が同じ因数[1]約数と同じ意味と思って大丈夫です！を持っているときに、その因数をくくります。
何言っているのか分かりにくいですね。
実際にやってみましょう。
共通因数でくくろう！
＜例題＞
因数分解してみましょう。
\(ax+ay\)
この時同じ文字が見えますね。
この時の\(a\)のことを共通因数と言います。
この式を因数分解してみると、
\(a(x+y)\)となります。
こんな感じで因数分解することを共通因数でくくると言います。
文字が共通因数の場合は分かりやすいのですが、共通因数が数字の場合になるとちょっと難しくなります。
今度は数字が共通因数の場合をやってみましょう。
＜例題＞
因数分解しましょう。
\(14x+21y\)
見た目には同じ因数が見当たりませんね。
でも、この時14と21はどちらも7を約数として持つので7が共通因数になります。
7でくくると、
\(7(2x+3y)\)となります。
数字の場合は共通因数が見た目では分からないので数字を見たらその数字を素因数分解とまでいかなくても積の形で見ることができれば共通因数は見つけやすくなります。
この時や14を\(14=7\times 2\)と見て、21を\(21=7\times 3\)と見ることができれば簡単に共通因数を見つけることができます。
この共通因数でくくるという過程は因数分解の1番の基本になります。
因数分解の問題が出たら1番はじめにすることは共通因数を探すことです。
これを忘れると解けない問題があるので絶対に忘れないようにしてくださいね！
\(x^2+(a+b)x+ab=(x+a)(x+b)\)を使って因数分解をしよう
この公式のポイントは\(x\)の係数のところが\(a\)と\(b\)の和、定数項のところが\(a\)と\(b\)の積になっている点です。
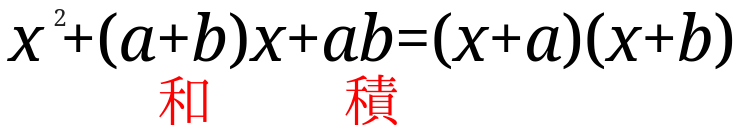まずは例題で見ていきましょう！
＜例題＞
因数分解しましょう。
\(x^2+5x+6\)
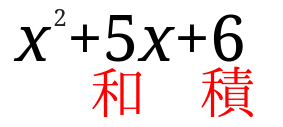
こんな感じに見えますか？
つまり、足して5掛けて6になる2数を探しましょう。
この2数を探す時のコツは掛けて6になる方から探すことです。
積の方を必ず利用しましょう。
なぜかというと積の方が通り数が少ないためです。
今回の因数分解では数字が小さいためどちらでいっても変わりはありませんが、必ず積の方を利用して考えましょう。
それではもう一題やってみましょう。
ちょっと難しくなりますよ。
＜例題＞
因数分解をしましょう。
\(x^2-10x-24\)
先ほどと同じように考えましょう。
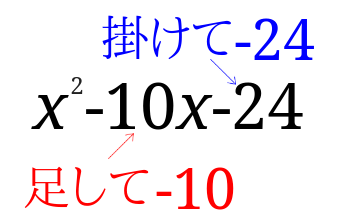
こんな感じに見えますか？
さらに数字を詳しく見てみましょう。
まずは積の方･･･今回で言えば-24から考えます。
この時に注目したいのはまずは符号[2]プラスやマイナスのことです。です。
-24ということは、この時の2数は正の数と負の数と言うことが分かります。
正の数と負の数を足して-10になるということは、その2数の絶対値の差が10ということになります。
つまり掛けて24になる数のなかで、その2数の差が10になるものを探せばいいということになります。
探してみると2と12が掛けて24、2数の絶対値の差が10なので条件に合う数が見つかりました。
あとはどちらか一方を負にすればいいです。
たして-10ということなので、探していた2数は-12と2ということになります。
答えは\( (x+2)(x-12)\)となります。
\(a^2+2ab+b^2=(a+b)^2\)を使って因数分解をしよう！
例題を見ながらやっていきましょう
＜例題＞
因数分解をしましょう。
\(x^2+14x+49\)
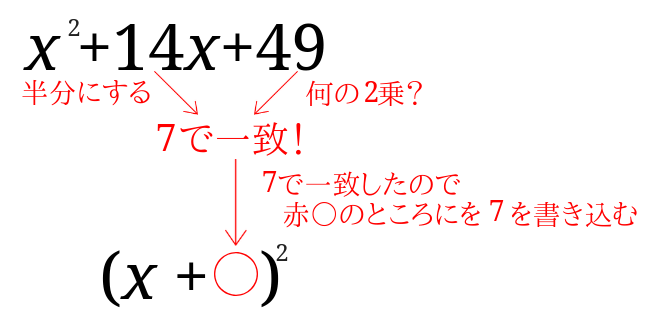
上のようにして解くと、答えは\( (x+7)^2\)となります。
文章にすると難しいので画像にしてみました。
慣れるととっても簡単ですが、慣れるまでは結構めんどくさいですね。
答えは\( (x+7)^2\)となります。
\(a^2-b^2=(a+b)(a-b)\)を使って因数分解をしよう！
例題を見ながらやってみましょう。
＜例題＞
因数分解をしてみましょう。
\(x^2-25\)
項の数が2個で間の符号がマイナスであることを確認しましょう。
この時に2乗マイナス2乗になっていることを確認します。
例題の式であればこんな感じに見ます。
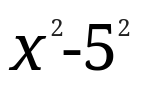
エックス2乗マイナス5の２乗になっていますね。
これが確認できたら、\(a^2-b^2=(a+b)(a-b)\)を使うことができます。
公式の形はこんな感じで見ると分かりやすくなります。
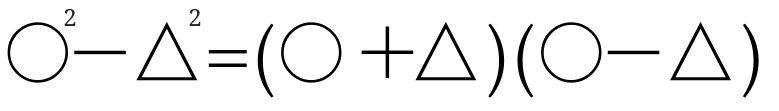
○や△が入ってきたこの公式の使い方ですが2乗マイナス2乗になったら、こんな感じに見てみましょう。
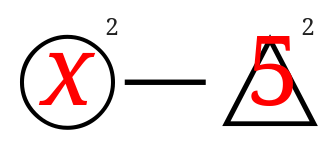
○の中に\(x\)、三角の中に\(5\)が入りました。
例題では\(x\)の2乗マイナス5の2乗になったので、○のところに\(x\)を△のところに5を書き込めばOKです。
後は先ほどの公式の
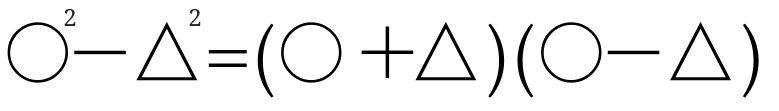
に入れてしまえばOKです！
○に\(x\)、△に\(5\)を入れると・・・
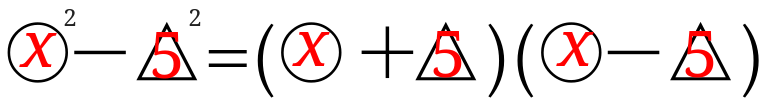
といった感じになりました。
よって。答えは\( (x+5)(x-5)\)ということになります。
これで中学校で習う因数分解の公式はすべてです。
因数分解の公式の使い方が分かったらあとはなれるだけです。
慣れないと解けないので頑張って慣れてくださいね！
まとめ
今回は因数分解の公式の使い方をしました。
公式を覚えたくなると思いますが、覚えてもあまりうまく使えないと思います。
まずはしっかり公式の使い方を覚えてくださいね。
やみくもに練習してもなかなかうまくならないのでまずはコツをしっかりつかむようにしましょう。
練習問題をたくさんするのは、公式の使い方を覚えてからするとスムーズに進みます。
