小学5年生で習う約数。
計算問題と違って特別な式があるわけでもなく、全部を書き出さないといけなかったりします。
小さい数字の約数をすべて書き出す分には適当にしてもなんとかなることが多いのですが、元の数字が大きくなると大変になります。
調べる数字が多くなり、漏れが出てしまうことも…
今回の記事では約数や公約数をもれなく自信をもって効率的に書き出す方法をやっていきます。
約数ってどんな意味?
まずは約数が何か分からないと、約数の書き出しようがありません。
約数とはある数を割り切ることが出来る数のことです。。
例えば、6の約数を考えると、6を2で割ると\(6\div 2=3\)となり割り切れます。
このとき2で6を割り切ることが出来たので、2は6の約数ということになります。
さらに、6を4で割ってみます。
\(6\div 4=1\cdots 2\)となり6は4では割り切れないことが分かります。
つまり4で6を割り切ることが出来なかったので、4は6の約数ではないということが言えます。
これで約数がどんなものか大体わかったでしょうか。
次は効率のいい約数の書き出し方をやっていきます!
約数の調べ方
約数がどんなものか分かったら次は約数の調べ方をしていきましょう。
約数をすべて書き出す問題はうまく漏れがないように約数を丁寧に書き出していくことが大切です。
適当にするとやはり漏れが多くなりますし、小学生の場合だと特にそれが多くなったり・・・
約数をもれなくしっかりすべて書き出せる方法をしていきますね。
<例題>
12の約数をすべて書き出しましょう。
約数を書き出す前に下の図のように横に一本の直線に線を引きます。
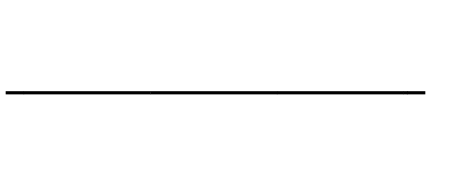
\(12\div 1=12\)なので12を1で割ると割り切れるので、1は12の約数ということになります。
1は12の約数なので図のように1を書き入れましょう。
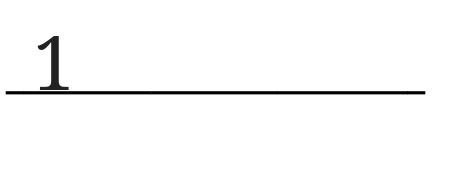
次に1の下に12を書き入れます。
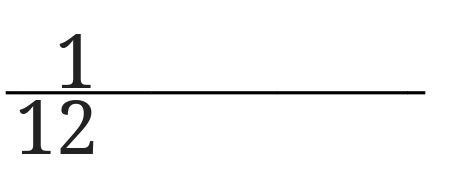
1の次は2なので12を2で割ってみます。
\(12\div 2=6\)となるので割り切れました。
1の時と同じように直線の上に2を書き入れます。
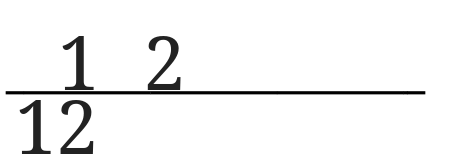
次に2の下に6を書き入れます。
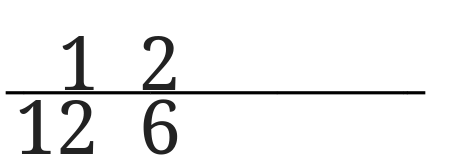
同じようにして、4まで書き込んでみました。
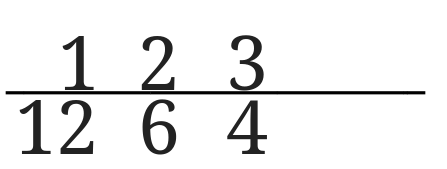
ここで注目してほしいのは、上の数字と下の数字を掛け合わせるとすべて12になるように書いていくということです。
例えば下の図のようになった場合、
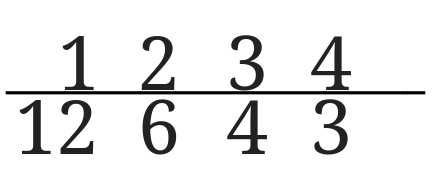
上の数字が下の数字より大きくなれば同じ組の組み合わせ(今回は3と4)が2回出たことになるので、その手前でストップです。
書き出した数字をすべて書くと答えになります。
きちんと答案には
$$1,2,3,4,6,12$$
という風に書くようにさせてください。
たまにその横に線を回答欄に引いてそこに約数を書いちゃう子がいますのでそれはダメと教えてあげてくださいね。
そんな風に書いてしまうと、おそらく学校の先生から減点か誤りとされてしまいます。
イメージとしてはこの書き方は計算問題の筆算のようなもので、答えのところに書くものではないので注意しましょう。
約数が求められるようになったら次は公約数を求めてみましょう!
公約数の簡単な求め方は?
<例題>
20と30の公約数を求めましょう。
求め方は大きく分けて2通りあります。
1つ目の方法はそれぞれの約数をすべて書き出してしまうという方法です。
早速やってみましょう。
20の約数を書き出してみると、
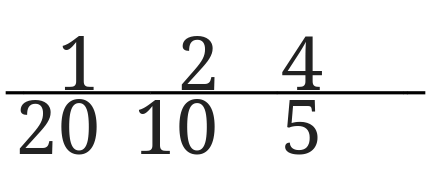
20の約数は1,2,4,5,10,20ということになります。
同じように30の約数も書き出してみます。

30の約数は、1,2,3,5,6,10,15,30ということになります。
最後に下の図のように同じ約数に印をつけて、20と30の公約数は1,2,5,10ということになります。
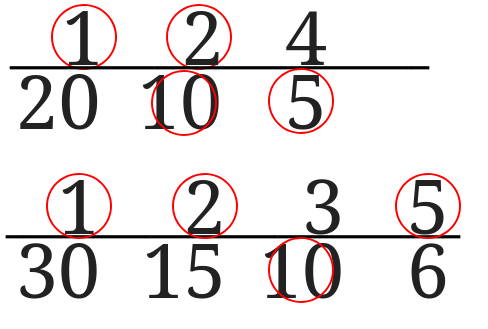
次は2つ目の方法でやってみます。
これは先に最大公約数が分かっているときに使えるやり方です。
20と30の最大公約数は10なので、10の約数を書き出してみます。
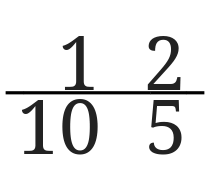
つまり20と30の公約数は1,2,5,10ということになります。
最大公約数の約数は公約数になるので先に最大公約数が分かっていたら使うように出来ればOKです。
まとめ
今回は約数や公約数の求め方をしました。
大抵、公立小学校で習う約数・公約数の場合は大抵すべての約数を書き出した方が早いです。
できる子の場合は素因数分解なども使えるようにしておくのがおすすめではあります。
しかし素因数分解を本格的に使うのは高校生の内容がメインになります。(中学受験では使うこともありますが…)
まずはきちんと書き出せるようにしておけば大丈夫ではないでしょうか。




