中学2年生では合同な図形を習い、中学3年生では相似な図形を習います。
基本図形の問題は難しくなりがちなので嫌われがちなのですが、中学3年生で習う相似な図形を習ってからは図形の問題の難しさが大きくアップします。
特に中学3年生の模試では、相似な図形が入ってくると問題の難易度が上がります。
しかし、分かると面白いということで図形の問題が好きになる子もいます。
今回は相似な図形の基礎となる三角形の相似条件を扱っていきます。
相似な図形って
そもそも相似な図形とはどんな図形でしょうか。
簡単に言うと同じ形の図形のことを相似な図形といいます。
大きさは違ってもいいということです。
イメージするなら、拡大コピーや縮小コピーをイメージすると分かりやすいです。
図形を紙に書いてその図形を拡大コピーや縮小コピーしてみましょう。
そこでコピーしたものと元の図形は相似な図形[1]そのまま拡大も縮小もせずにコピーすると、合同な図形のコピーができあがります。。となります。
相似な図形に関するイメージはこんな感じで大丈夫です。
それでは、三角形の相似条件に付いてみていきましょう。
三角形の相似条件
三角形が相似な図形になるときの条件を見ていきましょう。
・3組の辺の比がすべて等しい
・2組の辺の比とその間の角がそれぞれ等しい
・2つの角が等しい
どんな条件か1つずつ見ていきましょう。
3組の辺の比がすべて等しい
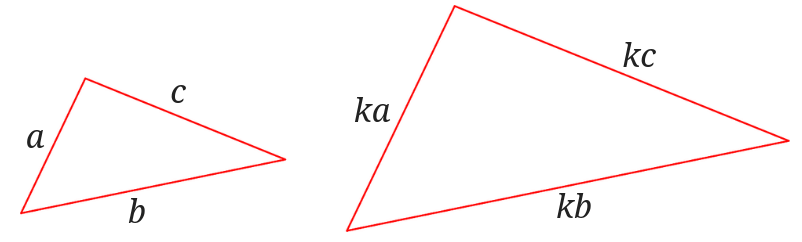図のように対応する辺の比を見てみるとすべて同じになっている三角形は相似だということです。
合同条件の3組の辺がすべて等しいの相似バージョンという感じですね。
この条件を見つけるには三角形の3辺の比を最も小さい自然数の比に直しておくと気付きやすくなります。[2] … Continue reading
というよりも、そうしないと気付くのは難しいのではないでしょうか。
もしこの条件を使う問題が受験に出たら、相似であることに気づくことそのものが難しくなると思います。
2組の辺の比とその間の角がそれぞれ等しい
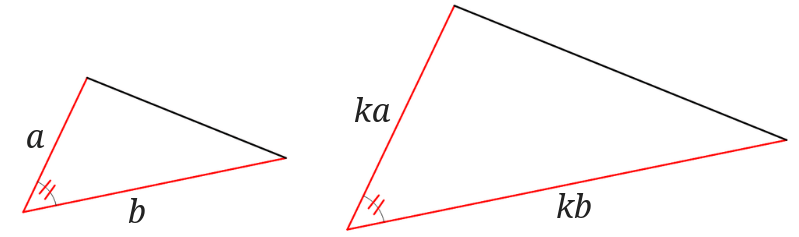図のように1つの角とその角を挟む2組の辺の比が等しいときに三角形は相似だということです。
合同条件の2組の辺とその間の角が等しいと似ているので覚えやすいですね。
角が等しいということは簡単に見つけられると思いますが、この条件も辺の比が等しいことに気づくのが大変。
この条件に気づくのためには、「3組の辺の比がすべて等しい」の時と同じで辺の比をなるべく小さな自然数の比にしておくことです。
この条件も相似であることに気づくのが難しい条件です。
きっちり辺の比を見るようにしておくといいですね。
2つの角が等しい
図のように2つの角が等しいときに三角形は相似だと言えます。
この条件は今までの条件と比べてみるとちょっと異質ですね。
今までは必ず辺が条件に入っていたのですが、角しかありません。
しかも2つしか条件がありません。
合同条件、相似条件のなかでも、条件が2つしかないのはこの「2つの角が等しい」という条件だけです。
ちなみに実際の受験などで頻出なのはこの条件です。[3]これ以外の相似条件がでたときは気づくのがとても難しいです。
辺の比が関係なく2角のみが等しければいいということで、見つけやすい相似条件です。
まとめ
今回は三角形の相似条件を3つご紹介しました。
証明問題ではそのまま書かないといけないのできっちり丸暗記してください。
合同条件と比べてると表現が異なる点があるのでそこには特に注意です。
うろ覚えで試験中に書こうと思うと、迷うことになること間違いありません！
きっちり書き出すところまで練習してくださいね。
