平方根って妙な数ですよね。
文字のような、数字のような…
とりあえず慣れて解ければいいやみたいな感じになりがちです。
そもそもなぜ平方根、ルートなんてものが生まれたのでしょうか。
そんなことを考えながら理解を深めていきましょう。
平方根とは
平方根とはなんでしょう?
例えば+3や-3を2乗すると9になります。
このときの+3や-3を9の平方根といいます。
つまり2乗するとある数になる数を平方根というってことです。
そんなに難しくなさそうですね。
それでは例題をしてみましょう。
<例題>
次の数の平方根を求めましょう。
①16 ②25
①は2乗して16になる数を探せばいいということです。
つまり、+4と-4ですね。
同様に②は+5と-5になります。
基本的に平方根は2つある[1]0のみ平方根が0の1つのみになります。ので注意しましょう。
これを中間考査や期末考査といった定期考査で忘れると本当に大変です。
大問1つが全滅…なんてこともあるので、平方根は2つあることを忘れないようにしましょう。
ちょっと難しくなりますよ。
<例題>
次の数の平方根を求めましょう。
③2
しばらくは平方根のうち正の数のほうだけ求めることにします。
負の数まで考えるとややこしくなってしまうので…
2乗して2になる数を探せばいいということですね。
1を2乗すると1、2を2乗すると4…
ということは2乗して2になる数は1と2の間にあるということになります!
それでは1と2の間の数で2乗して2になる数を探してみましょう。
\(1^2=1\)
\(1.1^2=1.21\)
\(1.2^2=1.44\)
\(1.3^2=1.69\)
\(1.4^2=1.96\)
\(1.5^2=2.25\)
\(1.6^2=2.56\)
\(1.7^2=2.89\)
\(1.8^2=3.24\)
\(1.9^2=3.61\)
\(2^2=4\)
あれ?
ありませんね。
1.4と1.5の間にあることは分かりましたが丁度の数が見当たりません。
またここで考えたいのは、同じ数を2回かけても下一桁が0になることはありません。
つまり、小数で2乗して2になる数を書ききれないということですね。
それでは分数はどうでしょうか?
\(frac{b}{a}\)を2乗したら2になるとしましょう。
元の分数の\(\frac{b}{a}\)はこれ以上約分できない分数だとしますね。
つまり\(a\)と\(b\)には1以外の公倍数がないということです。[2]互いに素といいます。
\(\frac{b}{a}\)を2乗してみると\(\frac{b^2}{a^2}\)となります。
これが2になるためには約分して分母の\(a^2\)を消さないといけないのですが、そもそもの条件で\(a\)と\(b\)には公約数がないので約分することができません。
ということは、2乗して2になる数は分数では表せないということになってしまいますね。
さて困りました。
2乗して2になる数は小数でも分数でも表すことができないということになってしまいました。
そこで、そういう数字がないのであれば作っちゃえということでできたのが√です。
2乗して2になる数を\(\sqrt{2}\)と書くことにしました。
平方根はなぜ必要?
平方根はなぜ必要なのでしょうか。
実生活では必要ないという方もいると思いますが、どうしたら平方根が生まれるのかなぁということについて考えてみます。
平方根は2乗してある数になる数のことを言います。
ということはある数を正方形の面積、2乗してある数になる数を正方形の1辺とみることができます。[3]ここでは正の数についてのみ考えてみます。
つまり面積が\(4cm^2\)の正方形を考えると1辺が\(2cm^2\)の正方形とみることができます。
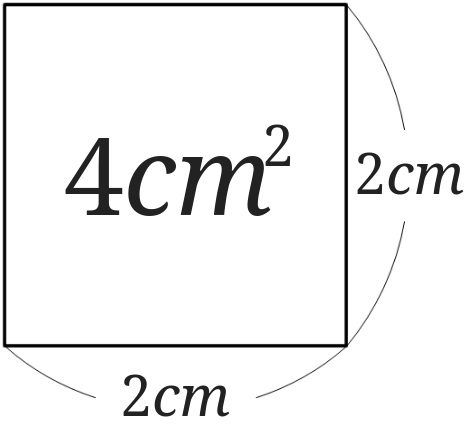
ここで先ほどの面積が\(2cm^2\)の正方形を考えてみましょう。

この時の1辺の長さは何\(cm\)でしょうか。
1辺の長さは、2乗して2になる数なので\(\sqrt{2}cm\)ということになります。
小数でも分数でもきれいに表すことができないので√という記号を使って表すことにしたんですね。
2乗してある数になる数を\(\sqrt{ある数}\)と書くことであらわすことにしたということです。
ちなみに2の平方根は?と聞かれた時の答えは、\(\pm \sqrt{2}\)ということになります。
√を使って書いても\(\pm\)を忘れないようにしましょう。
平方根は基本2つありますよ。
まとめ
今回は平方根についてでした。
どうしても公式の丸暗記的なことになりがちなのですが、正方形をもとにイメージするとちょっと親しみが持てるのではないでしょうか。
2乗するとある数になる数があるとき、ある数を面積、2乗するとある数になる数を1辺と考えるとイメージしやすくなります。
のちの計算も少しイメージできるだけで、やりやすくなると思いますよ。




