3点を通る円と外接円の作図

円って不思議な図形ですよね。

いろいろな性質がありますが、今回は3点が分かっているときの円の作図の仕方についてしていきたいと思います。

これは結構できない子が多いです。

小学校の内容のはずですが、中学生でもかける子のほうが少ないのではないでしょうか。

高校生でも…

作図なんて出ないという子も意外と実はこの作図は使えるので中学生でも、高校生でもできたほうが良いです。

どこで役に立つのかというと図形の問題で使えるんですね。

三角形が与えられてるときにその三角形の外接円を描くときには重宝します。

なんとなく書くと意外と難しいんですよね。

答案を見てみると楕円になってしまっていたり、いびつすぎて図形が分かりにくくなってしまったり…

この作図があればフリーハンドで書くときも大まかな位置が分かるのでしゅっと外接円が書けるようになります。

それでは作図をしていみましょう。

3点が与えられた時の円の作図の仕方は？

作図の前にまず考えたいのは、円についてです。
円とはどんな図形でしょうか？
丸い感じではありますが、数学的には「中心からの距離が等しい点の集合」と考えます。
これはとても大事な概念なのでしっかり頭に入れておいてくださいね！
今回の作図でもこの概念をしっかり使っていきます。

今回の作図で必要になるのは、コンパスと定規なのであらかじめ準備してください。
あとは作図するための紙があればばっちりです。

まず紙に3点を適当に書いてみましょう。
この時注意してほしいのは、書いた3点が一直線に並ばないようにしましょう。
3点が一直線に並んでいると円が書けません。^[1] … Continue reading
この条件だけ満たしていれば基本的に3点を通る円を描くことができます。

こんな感じで3点を取ってみました。

それではどうやって書いていきましょう？
作図するときは「なぜそうすると作図できるのか」常に意識しながらすると作図がうまくなります。
今回は今書いた3点を通る円を描きます。
円とは「中心からの距離が等しい点の集合」でした。
ということは、それぞれの点と円の中心を結んだ線分の長さは等しいということが言えます。

これを作図にどのように生かしていくのかというと、まず3点のうちどれでもいいので2点に着目します。
この選んだ2点から距離が等しい場所に円の中心はあるはずですよね。

まずはこの2点から距離が等しい場所を作図してみましょう。
この2点を両端とする線分の垂直二等分線を書きましょう。

垂直二等分線って線分を2等分にして、さらにその直線が線分と垂直に交わる直線ってイメージがありますよね。
もちろん、間違いではありません。
しかしもう一つ意味を知っていると、作図がグッとうまくなります。

垂直二等分線の性質は、「線分の両端からの距離が等しい点の集合」という意味もあるんですね。
覚えておくとすごく役立ちますよ。

垂直二等分線を書くとこんな感じになりました。

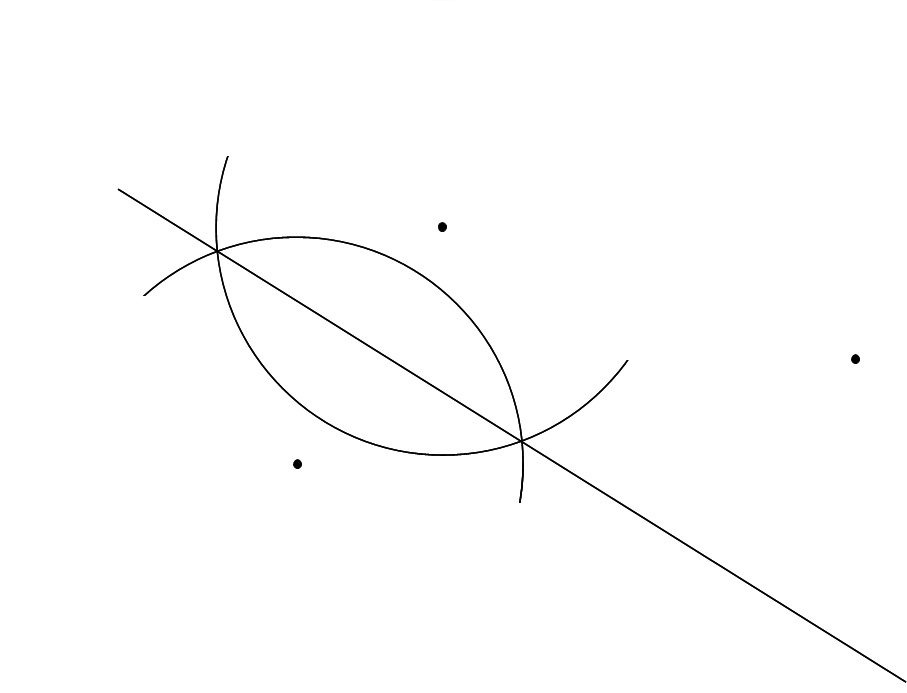
次にまた別の2点を選びます。
先ほど選んだ点の組み合わせと違う組み合わせであればOKです。
この2点を選んでみます。

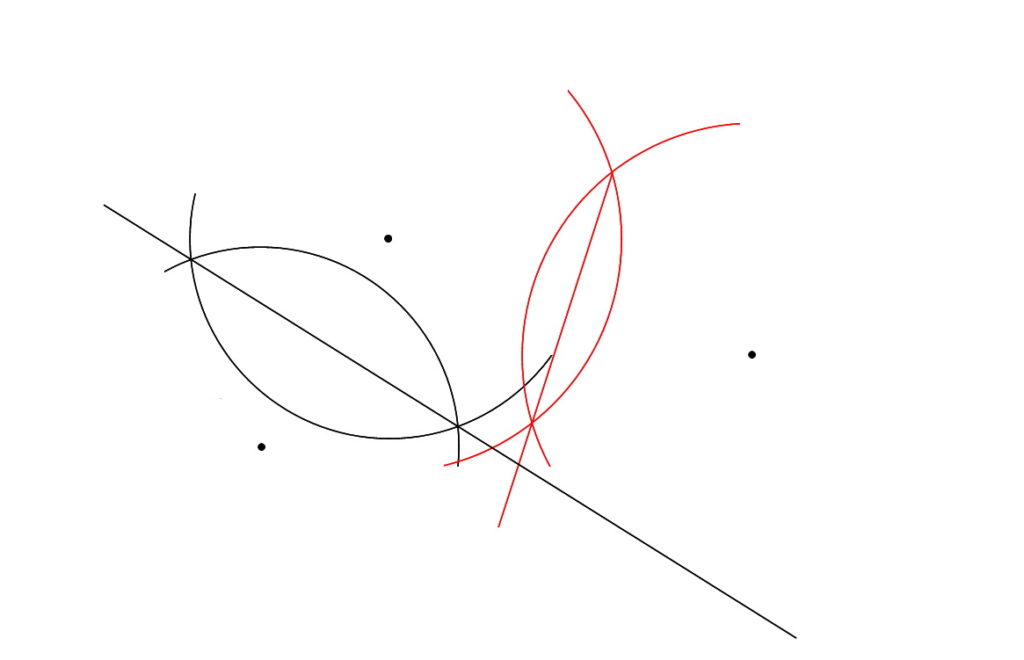
また同じように垂直二等分線を引きます。

するとこんな感じで交点が1つできましたよね？

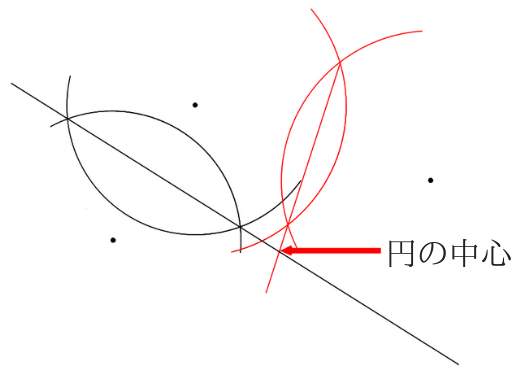
そこが円の中心ということになります。
あとはそこにコンパスを刺して、3点のうちの1点に合わせると3点を通る円を作図することができました。

外接円を作図しよう！

この作図の方法は三角形の外接円の作図にも使えます。
先ほどの3点を最初から結んであげると三角形になりますよね。
3点を通る円を作図するということは、三角形の3つの頂点を通る円を作図することと意味は同じですね！

同じようにすると三角形の外接円を作図することができます。
でも試験中にはコンパスがないということが多いと思います。
そんなときはフリーハンドで垂直二等分線を2本書いて円の中心を大まかに分かるようにします。
それから円をフリーハンドで書くと円の中心が分からないまま書いた外接円と、円の中心が分かる状態で書いた外接円は随分と違うと分かると思います。

図がきれいに描けるだけで問題を解きやすくなります。
あまりいびつな図を描いてしまうと見れば気づくようなところにも気づきづらくなり、図形が苦手…となりかねません。
逆に考えるときれいに図が書けることが図形の問題に強くなる1つの要因でもあるということです。

フリーハンドで図を描くにしても作図の手順をたどることで、きれいに図を描くことができます。

まとめ

今回は3点を通る円の作図でした。

まずは円の定義をしっかり頭に入れておくことが大事です。

円は「中心からの距離が等しい点の集合」でしたね。

ここがしっかり分かっていれば2点を選んで垂直二等分線を2本書けば円の中心が分かります。

しっかり作図できるようにしておきましょう。