√ってなかなか不思議な数ですね。
小数では書ききれないし、分数では表せない数です。
小数でも分数でも表しきれない√ですが、実は線分の長さでは表すことができます。
三平方の定理[1]ピタゴラスの定理と呼ばれたりもします。を使ってすると簡単に作れるのですがそれだと納得が得られにくいです。
計算してなるから作図ができたよね?って言われても、そうなんですか?って感じだと思います。
直感的に、ここの長さが√2!と納得できるように作図をしてみたいと思います。
平方根を正方形を使って作図してみよう。
平方根を正方形をうまく使って作図してみたいと思います。
三平方の定理などを使わずに算数のように考えて作図をする事を目指したいと思います。
√2の作図であれば面積が2の正方形を描くことができれば、その一辺が√2の長さと言うことは納得して貰いやすいです。
もちろん先に√2を2回掛けると2になる数だと言うことは納得しておかないと意味がありません。
ここのところは確実に理解・納得してから作図をすると理解が深まりますよ。
√2を作図してみましょう。
√2を作図してみましょう!
小数では書ききれず、分数では書けない\(\sqrt{2}\)…
それなら図で書いてみようというのが今回の企画です。
中学3年生の平方根を習った段階では三平方の定理はまだ知らないので、三平方の定理は使わずに線分を描きたいと思います。この方法だと小学生でもそんな数があるのかと納得する事ができます。
今回は面積が2の正方形を描いたときのその正方形の一辺が√2であるという形で描きたいと思います。
面積が2の正方形があればその1辺の長さが√2であるというのは、√の定義通りなので1番分かりやすいですし納得がいくのではないでしょうか。
まずは面積が1の正方形を描いてみましょう。
1辺の長さが1の正方形を描けばOKです。

こんな感じですね。
この正方形に対角線を1本引いてみます。
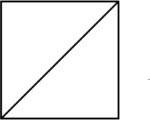
すると直角二等辺三角形が2つできました。
もとの面積が1だったので、2つの直角二等辺三角形の面積は\(\frac{1}{2}\)ということが分かりますね。
左上の直角二等辺三角形を赤く塗ってみます。

同じようにした正方形をあと3つ準備します。

赤く塗った直角二等辺三角形が正方形になるように並べてみます。

赤く塗った直角二等辺三角形の面積は\(\frac{1}{2}\)でした。
この赤い正方形は直角二等辺三角形4つからできています。
つまりこの赤い正方形は面積が2の正方形ということになります。
ということは、この赤い正方形の1辺の長さは\(\sqrt{2}\)ということになります。
\(\sqrt{2}\)を作図することができましたね。
√5を作図してみましょう。
√2の作図と同じように正方形を利用します。
√5を作図するというのは、面積が5の正方形を作図すれば、√5が作図できたことになります。
先ほどは正方形の対角線を利用しましたが、今度はちょっと一工夫してみます。
まずは正方形を2つ並べて長方形を作ります。

その出来た長方形に対角線を引きます。

対角線を引いたら上半分を赤く塗ってみました。
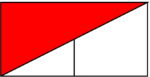
もとの長方形の面積が\(2\)なので色を塗った三角形の面積は\(1\)ということになります。
この長方形を4つ準備してみました。

この長方形をうまく組み合わせて面積が5の正方形を作ってみたいと思います。
こんな感じで並べると面積が5の正方形ができました。
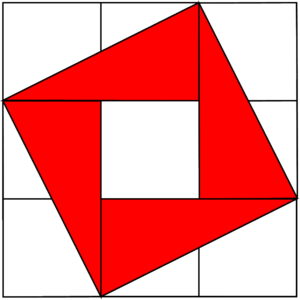
真ん中に穴がぽっかり開いていますが、そこは1辺が1の正方形なので面積が1です。
その周りの色を付けた三角形の面積は1だったので、その三角形が4つあります。
面積が1の正方形と、面積が1の三角形4つでできた正方形なので面積が5の正方形ができました。
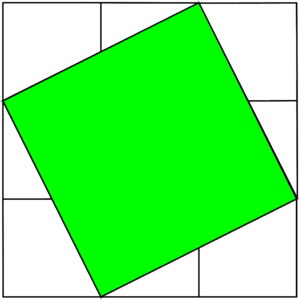
つまり出来た正方形の1辺の長さが√5ということになりますね。
まとめ
今回は数字では表しにくい√2や√5を作図して長さで示してみました。
意味が分かりにくいルートですが、こうして作図してみると親しみもわきますね。
三平方の定理を使っていないので直感的にも納得がしやすいのではないでしょうか。
この作図が直接役に立つということはあまりないと思いますが、平方根に対する理解は深まると思います。
やはりイメージしやすいものとイメージしずらいものであれば、イメージしやすいもののほうがやりやすいし、理解しやすいものです。
またこのやり方だと小学生にも理解させることができます。
小学校では習わないのですが、小学生が√を見かけるところが1か所あります。
それは電卓です。
「√のボタンはなぜ連射すると最後は1になるのですか」と聞かれることがあります。
男の子に多い感じですね。しっかり電卓で遊んでいると発見してしまうのでしょう。
ちょこちょこそんな質問されることがあるのですが、「もっと先で習うから知らなくてもいいよ」とか「そういうもんだよ」と答えるよりも、小学生の知的好奇心を満たせるのではないでしょうか?
√のボタンは正方形の1辺の長さを出すボタンってイメージになってしまいそうですが…
References
| ↑1 | ピタゴラスの定理と呼ばれたりもします。 |
|---|




