相似な図形の面積比と三角形の辺の比から求める面積比

今回は相似な図形の面積比や色々な三角形の面積比について考えていきます。

相似だということが分かれば相似比から簡単に面積比を求めることができるという優れものです。

他の三角形の面積比を出す公式もとても役に立つのでしっかり覚えて使えるようにしましょう。

相似な図形の面積比

下の図のような相似な三角形があります。

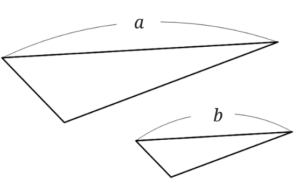
2つの図形の相似比が$a:b$のときの面積比は$a^2:b^2$となります。
相似比の2乗が面積比ということです。^[1]相似な図形の面積比は相似比の2乗と覚えておけばいいと思います。

例えば、相似比が$2:3$の図形があったときの面積比は$4:9$ということになります。
難しくありませんね。
ちょっと練習してみましょう。

＜例題＞
相似比が$5:9$の2つの三角形があります。
この三角形の面積比はいくらになりますか。
また小さい三角形の面積が$75cm^2$のとき大きな三角形の面積は何$cm^2$ですか。

相似比が$5:9$なので、面積比はこの比の2乗なので$25:81$となります。

次に大きな三角形の面積を求めます。
面積比が$25:81$ということが分かっているので、$75\times \frac{81}{25}=243$となるので、大きいほうの三角形の面積は243ということになります。

相似比が分かっていれば面積比は簡単に求められます。
今度は相似比が与えられていない場合をやってみましょう。

＜例題＞
下の図のような2つの三角形があります。
2つの三角形の面積比を求めましょう。

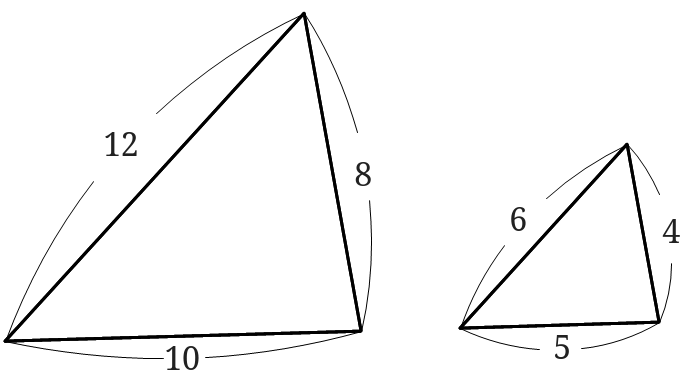
この2つの図形は相似な図形になるのですが、分かりますか。
対応する辺の比がすべて1：2になっているので相似といえます。

対応する辺の比が1：2なので、相似比は1:2ということですね。
面積比はこの比を2乗したものなので、$1:4$ということになります。

相似な図形の場合、相似比が分かってしまえば面積比を求めることはとても簡単です。
非常に便利な相似比と面積比の関係ですが、これが使えるのはあくまで相似な図形同士の間においてだけです。
相似な図形でない場合は成り立ちません。

ちょっと別の問題で見ていきましょう。

三角形の面積比と辺の比

＜例題＞
次の三角形の面積の比を求めましょう。

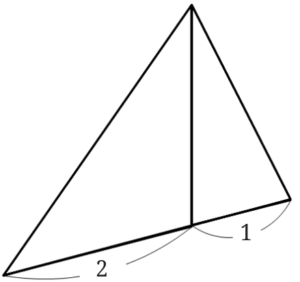
長さが1と2があることから、相似な図形同士のように相似比の2乗ということで面積比を$1:4$としちゃだめですよ。
相似比の2乗が面積比になるのは、相似な図形の間で成り立つだけで、相似ではない図形同士では成り立ちません。
習いたてのうちは相似な図形同士の場合相似比の2乗が面積比となるということの相似な図形同士の場合という条件が抜け落ちてしまうことが多くあります。
相似な場合ではなく、ある辺の2乗が面積比のようになってしまいこの問題のような問いに対しても2乗してしまう子がいます。
相似ではない時には2乗しても面積比にはならないので注意しておきましょう。

ちなみにこの2つの三角形の面積比は$1:2$となります。
この2つの三角形は高さが共通なので底辺の比がそのまま面積比になります。

ピンとこない子もいると思うのでもう少しきちんと見ていきますね。
高さを$h$とします。

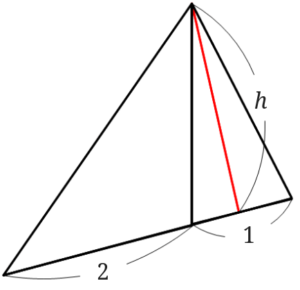
すると小さいほうの三角形の面積は$\frac{1}{2} \times 1\times h=\frac{1}{2}h$となります。
大きいほうの三角形の面積は$\frac{1}{2}\times 2 \times h=h$となります。
この2つの三角形の面積比なので、$\frac{1}{2}h:h$となり、$h$でどちらも割ると、$1:2$となり、面積比は$1:2$となりました。

いつもこんなことをするのは面倒なのでこれを公式化してみましょう。
図のような三角形があります。

三角形の1つの角から対辺に直線を引くと2つの三角形に分かれますね。

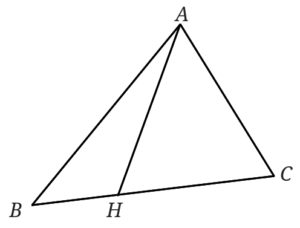
この時$BH=a$、$CH=b$とおきます。

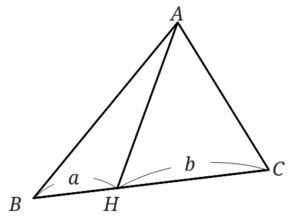
するとこの時の面積比は、$a:b$となります。
なぜかというと、高さを$h$とすると左側の三角形の面積は$\frac{1}{2}ah$、右側の三角形の面積は$\frac{1}{2}bh$となります。
面積比は、$\frac{1}{2}ah:\frac{1}{2}bh=a:b$となりますね。

図形の問題では非常によく使いますのでしっかり相似な図形の面積比としっかり区別して覚えておくようにしましょう。
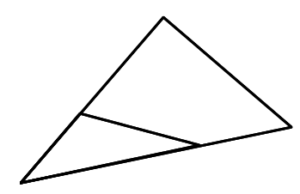
この面積比を使う場合は必ず三角形の角を通る直線じゃないとだめですよ。
下の図のように三角形の角を直線が通っていない場合は使えないので注意しておいてくださいね。

ちなみにこの三角形の中に三角形がある図形の面積比にも公式があるんですね。

三角形の中の三角形の面積比

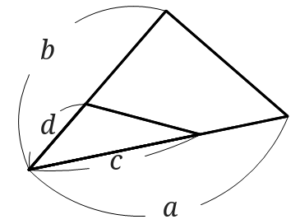
長さを図のように定めます。

すると、大きい三角形:小さい三角形=$ab:cd$となります。
意外と単純なので覚えやすいですね！
受験では大問1で出てくることがあるので覚えておくと楽に答えが出せますよ。
勿論知らなくても出せますが結構使える公式なので覚えてくださいね。

三角形の中の三角形の面積比の証明

先ほどの大きい三角形:小さい三角形=$ab:cd$の証明をしてみましょう。
下の図のように記号を打ってみました。

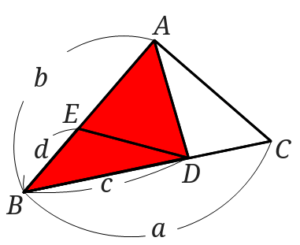
$\triangle ABC$を使って$\triangle BDE$（小さい三角形）の面積を表してみます。
下の図のように点$A$と点$D$を結びます。
$\triangle ABD$（赤い三角形）の面積を$\triangle ABC$を用いて表します。
$\triangle ABD=\frac{c}{a} \triangle ABC $
$\triangle BDE$（黄色い三角形）を$\triangle ABC$を使って表してみます。
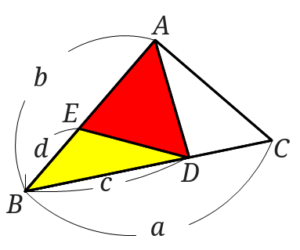$\triangle BDE=\frac{d}{b}\times \frac{c}{a} \triangle ABC $
$$\triangle BDE=\frac{cd}{ab} \triangle ABC $$$$\frac{\triangle BDE}{\triangle ABC}=\frac{cd}{ab}$$$$\triangle ABC: \triangle BDE=ab:cd$$となり、大きい三角形:小さい三角形=$ab:cd$が成り立つと言えますね。