最小公倍数と最大公約数から元の数を求めるには互いに素な数と共通因数が鍵！

素因数分解と倍数・公倍数、約数・公約数は密接な関係があります。

2つの数が与えられたり3つの数が与えられたりして、最小公倍数や最大公約数を求めるのはそんなに難しくはありませんね。

しかしこれが逆になるとかなり難しくなります。

最初に与えられる数字が最小公倍数と最大公約数が与えられ、元の数を求める問題です。

数学が苦手な子だと丸暗記に走りがちですがきちんと理解すればすんなり解くことが出来るようになります。

まずは2つの数から最小公倍数と最大公約数を求める過程から、どのようにすれば最大公約数と最小公倍数からもとの数を出すことができるのか考えていきましょう。

連除法を使って最大公約数と最小公倍数を求める！

最大公約数と最小公倍数から、もとの数を考えても分かりにくいと思うので、まずは2数が与えられたときの最大公約数と最小公倍数をもとめるところからやってみます。

＜例題＞
24と84の最小公倍数と最大公約数を求めましょう。

まずは連除法(はしご算)を使って、最小公倍数と最大公約数を求めます。

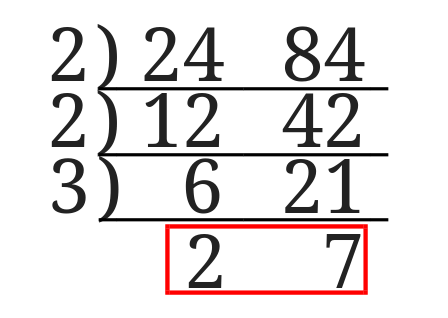
赤で囲んだところの数が公約数を1しか持たない^[1]こんな関係を互いに素といいます。ようになるまで割りましょう。

まずは最大公約数を求めます。

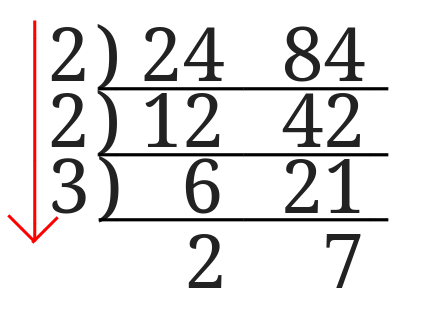
最大公約数を求めるには赤の矢印のところの数を全て掛け合わせると出すことが出来ます。
$2^2\times 3=12$
つまり24と84の最大公約数は12ということが分かります。

続いて24と84の最小公倍数を求めます。

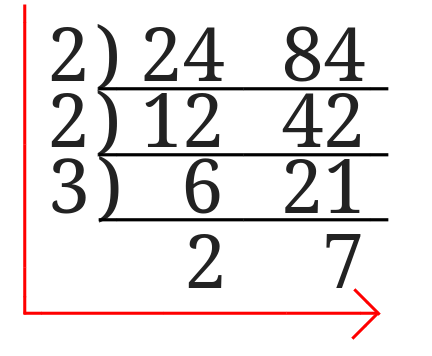
図矢印の通りに数を掛けていくと最小公倍数を求めることが出来ます。
つまり$2^2\times 3\times 2\times 7=168$となるので24と84の最小公倍数は168ということになります。

最大公約数と最小公倍数は連除法で分かる!

24と48の最小公倍数は168、最大公約数は12ということが分かりました。
今度は最小公倍数が168で最大公約数が12である2数を求めてみましょう。

＜例題＞
最小公倍数が168で最大公約数が12である2数を求めてみましょう。
ただし2数の和は106とします。(複数答えがでてしまうので、条件を追加しました。)

連除法の計算からなぜ最大公約数や最小公倍数を求めることができるのかを考えてみましょう。
連除法では与えられた2数のどちらも割り切れる数を左側に書きいれます。

互いに素な数と共通因数が鍵！

ということは左側に並んだ数は2数の共通因数ということが言えます。

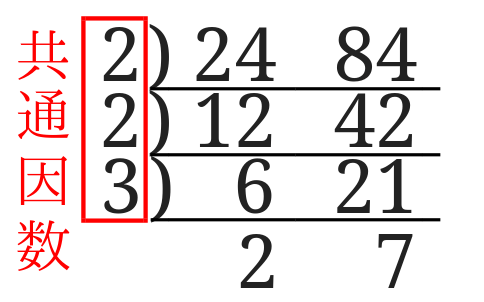
一番下に来た数は共通ではない因数ということになります。

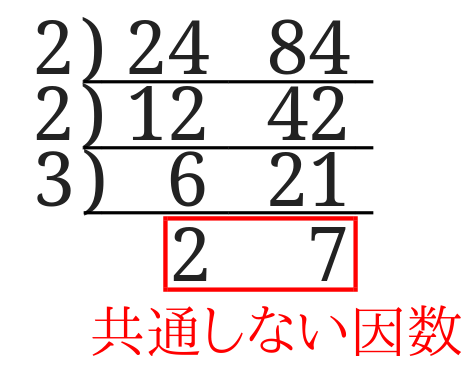
ということは、連除法を使うと与えられた数を共通因数と共通ではない因数の積に表すことが出来ます。
24と84の場合だと
$$24=(2^2\times 3)\times (2)$$
$$84=(2^2\times 3)\times (7)$$
と書くことが出来ます。

このままだと分かりにくいので、一般的に考えてみましょう。

連除法で2つの求める数$a,b$の最大公約数と最小公倍数を出すことにすると、

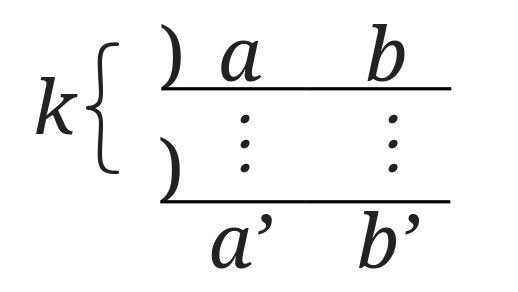
という形になります。
$a’$と$b’$はお互いに1以外に公約数を持たない数^[2]互いに素です｡です。
$k$は$a$と$b$の共通因数です｡

すると
最大公約数は$k$、最小公倍数は$ka’b’$と表せますよね。
このことから最小公倍数を最大公約数で割ると$a’b’$になります。

また
$$a=ka’$$
$$b=kb’$$
と表すこともできます。

例題では最大公約数は12、最小公倍数は168が与えられているので、最小公倍数を最大公約数で割ると$a’b’$にあたる数が出てきます。
$$168\div 12=14$$
となるので、$a’b’=14$といえます。
つまり$a\leqq b$とすると$ (a’,b’)=(1,14),(2,7)$となります。
$(a’,b’)=(1,14)$のとき
$a=ka’$なので$a=12$,$b=kb’$なので$b=168$となります。
$a$と$b$の和が106にならないので不適となります。

$ (a’,b’)=(2,7)$のとき
$a=ka’$なので$a=24$,$b=kb’$なので$b=84$となります。
$a+b=106$になるのでこれは問題に合うということになり、求める2数は$24$と$84$ということになります。