高校受験では平面図形や空間図形が花形です。
証明問題や相似の問題、体積の問題など受験のなかでも難問が登場しやすい単元です。
それでも数学がどんなに苦手でも必ず得点したい問題があります。
それがねじれの位置の数や辺などを答える問題です。
出題されるとすると空間図形の1番に出題されますが、ここは単元唯一の得点の取りどころ!
でもちょっとした勘違いなどで落としてしまう子もたくさんいます。
そうならないようにするにはどのようにすればよいでしょうか?
今回は空間図形の問題でねじれの位置にある辺をもれなく見つけるコツについて書いていきます。
平行とねじれの位置の違い
平面図形では辺の位置関係は大きく分けて2種類あります。
それは「平行」か「交わる」の2つです。
これはなにか補足をしなくても分かるのではないかと思います。
それが空間図形になると辺の位置関係が3種類になります。
「平行」「交わる」は平面図形と同じなのですが、空間図形になると「ねじれの位置」が辺の位置関係に追加されます。
交わるというのは大体分かると思いますので、「平行」と「ねじれの位置」について考えていきましょう。
まずは平面図形で考えていきます。
はじめに、意識しておきたい前提があります。
辺の位置関係を考える際はすべての辺は線分ではなく直線として考えます。
平行を平面図形内で探す!
例えば下のような台形があります。
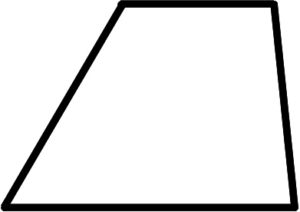
上と下にある辺は直線[1]直線とはずっと終わりがなく延々と伸びているまっすぐな線のことです。として考えても交わることがないことから、平行だと言えます。
一方で右と左の辺は見た感じ交わっていませんよね?
交わらないから平行だとは言えずあくまで直線で考えても交わらなければ平行と言えます。
この台形の右の辺と左の辺は辺を伸ばしてみると交わってしまうので平行ではありません。
でも、ここは言われなくても大丈夫ですよね?
ここで延長して交わらなければ平行と書いたのには理由があります。
平面図形で見た目交わっていないから平行と書く子はほとんど皆無なのですが、これが空間となると辺を延長することなく見た目が交わっていないことを理由に平行だと判断する子が増えます。
そのため、平面上でも辺は延長して交わってしまえば平行ではない!と覚えておいてくださいね。
ここの意識が空間図形のねじれの位置や平行を考えるときに役立ちます。
今度は空間図形で考えてみましょう。
平面から立体になるということですね。
立体になると、ねじれの位置という関係ができます。
なぜ立体になるとねじれの位置という位置関係が出てくるかというと平面図形内にはねじれの位置はありません。
このことは空間図形のなかでねじれの位置を探すときに大きなヒントになります。
平面図形にねじれの位置がないということは、同じ面にある辺同士がねじれの位置関係にあることはないということです。
これはミスをすごく減らせるので必ずイメージできるようにしておいてください!
それでは結局ねじれの位置とはどんな位置関係かというと、2直線が交わらず平行ではない位置関係を言います。
なんだか消極的な感じですね!
これがねじれの位置だ!って言えるとかっこいいんですけどね。
仕方ありません。
ねじれの位置を見つけるコツ!
ねじれの位置を見つけるのは正確にしたいですよね。
高校受験では絶対点のとりどころです。
数学が苦手だからと関数や平面図形、空間図形を捨てちゃう子が結構いますが、空間図形のねじれの位置だけは絶対に捨てちゃだめです!
数学の問題の中でもおいしい問題です。
空間だからってビビっちゃだめですよ。
それでは実際にねじれの位置を見つけていきましょう。
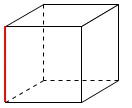
下のような立方体を元に考えます。
赤の辺のねじれの位置を考えます。
ねじれの位置を見つけるときは、「これがねじれの位置だ!」って感じで見つけちゃだめです!
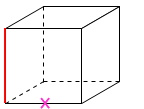
ねじれの位置を見つけるときは、必ず消去法で行きます。
ねじれの位置の関係にないと分かった辺には✖を付けていきます。
こんな感じですね。
それでは消去法で探しますよ!
①ねじれの位置は同じ平面上にないので、同じ面にある辺すべてにバツを付けます。
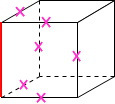
同一平面上にある辺すべてに✖を付けました。
②平行な位置関係にあるものを消します。
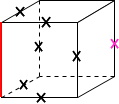
平行な位置関係にある辺にバツをしました。
①②をやってみて残った辺がねじれの位置になります。
ねじれの位置に○を付けてみました。
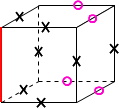
あとは問題文をきちんと見て判断しましょう!
ねじれの位置にある辺を具体的に聞かれているのか、それともねじれの位置にある辺の数を聞かれているのかで随分と答え方が変わってきますからね。
きちんと問題文を読むようにしましょう!!
まとめ
今回はねじれの位置の見つけ方のコツをしました。
ねじれの位置にある辺を見つけようとすると見落としが出たり、平行線をねじれの位置と勘違いしてしまう子がでやすくなります。
焦っても仕方がないのでミスが出にくい消去法で考えるようにしましょう。
ねじれの位置は同じ平面上にはないので同じ平面にある辺がねじれの位置の関係になる事はありません。
立体で考えると間違えやすくなるので平面で考えると間違えやすくなると思いますよ!
自分は大丈夫!って思っていても、高校受験本番だけ間違えたなんてことになったら大変ですからね。
かっこいい解き方ではなくあくまでもミスをしない解き方でしてくださいね。
消去法で考えることでミスが減るし、自信をもって答えが書けるのではないでしょうか。
References
| ↑1 | 直線とはずっと終わりがなく延々と伸びているまっすぐな線のことです。 |
|---|




