二次方程式や二次関数ではできないと困る平方完成。
なんだか中途半端な因数分解な感じの平方完成ですが、コツが分からないと路頭に迷いやすいです。
実際のところは、やり方さえ分かればそんなに難しくないですよ。
今回の記事では簡単に平方完成ができる見方について書いていきます。
平方完成の仕方
まずは平方完成の目的って何でしょう。
平方完成の目的は、\(x\)をひとまとめにして、カッコでくくることです。
そうすると、変数部分がひとまとまりになるので、頂点や軸などが分かります。
そう言われてなんことか、わかりにくいと思うので、実際に平方完成をしながら説明していきます。
それでは例題を見ていきましょう。
＜例題＞
次の式を平方完成しなさい。
①\(x^2+4x-5\)
②\(x^2+4x+5\)
平方完成のやり方1
①からみていきましょう。
平方完成をするときにみるのは、\(x^2\)の項と\(x\)の項のみみます。
定数項は完全に無視しましょう。
定数項をみると訳がわからなくなりやすいので注意が必要です。
この場合は\(x^2+4x\)だけを見て、\(-5\)については無視をしてくださいね。
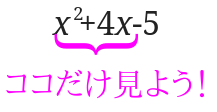次にチェックするのは\(x^2\)の係数です。
ここの係数が\(1\)であれば何もしなくてOK！
次に式を下に追加します。
こんな感じです。
定数項は全く触らないようにしてください。
次に空欄にしたところに数字を入れましょう。
\( (x+2)^2\)を展開すると\(x^2+4x+4\)となり\(+4\)が余分にでてきます。
\(-4\)を式に入れます。
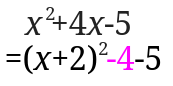
後は後ろの定数部分を整理します。
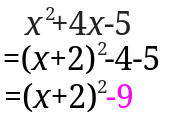ということで平方完成をすると\( (x+2)^2-5\)となりました。
平方完成のやり方2
違うやり方というほどではないのですが、もう1つ平方完成のやり方を説明しておきますね。
もう一度①を使ってします。
\(x^2\)係数が1であることを確認します。
次に\(xの係数\times \frac{1}{2}\)をして\(2\)乗した数を足して引きます。
\(x\)の係数の半分の2乗の数を足して引くと覚えてもいいですね。
始めの3つの項で因数分解をして、最後の2項の計算をして出来上がりです。
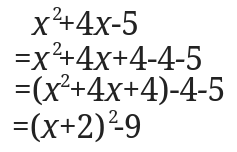どちらの方法も根本的になんの違いもないのでお好みの方法でやってみましょう。
②を平方完成します。
・やり方1
\(x^2+4x+5\)
\(=(x+2)^2-4+5\)
\(=(x+2)^2+1\)
やり方2
\(x^2+4x+5\)
\(=x^2+4x+4-4+5\)
\(=(x+2)^2+1\)
やり方はとちらでもお好みの方法でどうぞ。
どちらの方がいいということはないので好きな方法を選んでくださいね。
平方完成をする式に\(x^2\)の項に\(1\)以外の係数がある時
次に\(x^2\)に\(1\)以外の係数があるときの平方完成をしてみましょう。
＜例題＞
平方完成をしましょう。
③\(2x^2+4x+1\)
\(x^2\)に係数がある時はまずはその係数でくくります。
先程の仕方と同じで、\(x^2\)の項と\(x\)の項だけ見て、定数項は無視します。
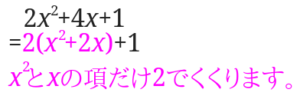次にカッコの中身の\(x^2+2x\)を平方完成します。
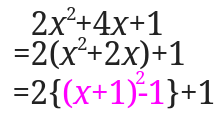中カッコ[1]小カッコ：() 中カッコ：{} 大カッコ：[] をはずします。
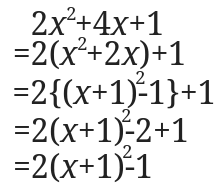これで出来上がりです。
順番にすればそんなに難しくありませんね。
平方完成をしようとしたらxがない？！
平方完成をしようとしたら\(x\)がない！？ってことがあります。
こんなときはどうしたらいいのでしょうか。
例題を使ってみていきましょう。
＜例題＞
平方完成しましょう。
④\(x^2+5\)
こんなときの平方完成ですね。
結論はこのままでＯＫです。
実際こんな問題はあまりないと思います。
あればそのままでいいのではないでしょうか。
本当に無理やり④平方完成をするとすると、\( (x+0)^2+5\)といった感じでしょうか。
うーん、ちょっとね…という感じになってしまいますね。
まとめ
今回は平方完成のやり方についての記事でした。
このやり方で係数に分数が入ろうがルートが入ろうが文字が入ろうがきちんとできます。
まずは流れ通りにやってみてくださいね。
\(x^2\)の項と\(x\)の項に注目し、定数項を無視することがポイントです。
ここをはずしてしまうと平方完成ができないということになってしまいます。
因数分解とは違うので注意が必要です。
平方完成の練習をするときは色々な問題をするよりもまずは同じ問題でいいのでしっかりやり方を確認しながらする方がいいと思います。
たくさん問題を解けばいいというモノでもありませんよ。
関連コンテンツ
References
| ↑1 | 小カッコ：() 中カッコ：{} 大カッコ：[] |
|---|
