二次方程式の解の個数を求める問題をみると使いたくなる公式は何ですか?
ほとんどの子が判別式を使うものだ!と答えると思います。
しかし、解の個数を求める方法は判別式だけではありません。
別の方法もあります。
単純に解の個数を求めるだけだと、判別式は優秀な公式です。
ただ、数学が苦手な方がちょっと難しい問題に出会っただけで手も足も出なくなる原因にもなることがあります。
今回の記事では判別式を使わない解の個数の出し方について書いてみたいと思います。
目次
二次方程式の解の個数が求められるもう一つの方法
解の個数を求める別の方法ってあなたは頭に浮かびますか?
もし別の方法が頭に浮かぶのであれば、数学が得意という方かもしれませんね。
その方法とは二次関数のグラフを書いて判断する方法です。
何かスーパー公式を期待された方ごめんなさい。
この二次関数のグラフを書くという方法は、判別式を使って解の個数を求めることと比較すると面倒くさいです。
だけど、私は数学が苦手な方にこそこの方法をおすすめしたいと思っています。
その理由は3つあります。
1、グラフが書けるようになる。
二次関数のグラフを書いて解の個数を判断するので当たり前と言えば当たり前です。
二次関数のグラフを迷わず書くことができますか?
二次関数のグラフを書くときに必要な情報をあげることはできますか?
グラフを書くことで、解の個数だけでなく、ちょっと難しい問題くらいは平気で対応できるようになりますよ。
2、グラフを書くことで何をしているのかイメージすることができるようになる。
判別式に代入して二次関数の解の個数を判断していくことはできます。
しかし、「で何?自分は何をしているの?」、「結局どういう意味」ってなっていませんか?
そうなんです。
判別式を利用して解く方法には覚えて代入するだけというメリットもありますが、自分のやっていることが分からなくなりやすいというデメリットもあります。
それがグラフを書いて求めるとグラフの形や位置などが分かるので応用問題でも対応しやすくなります。
3、式の扱いが上手くなる。
グラフは平方完成をしないと書きにくいです。
代入するだけで使える判別式と比較すると、グラフを書いて解く方が平方完成を通して式を扱うのが上手くなります。
またグラフを書く過程から、どの係数が何を意味するのかが分かるとぐっと理解しやすくなります。
それでは解の個数を求めるための二次関数のグラフの書き方について説明します。
二次関数のグラフの書き方のコツ
今回は解の個数を求めるために必要なグラフを書く時の情報について整理します。
必要な情報は2点です。
1、上に凸なグラフなのか下に凸なグラフなのか。
2、頂点の座標
二次関数のグラフが上に凸?下に凸?
1番のグラフの大まかな形が見えるポイントです。
見るところは、\(x^2\)の係数です。
\(x^2\)の係数が正の数であれば下に凸なグラフ。
\(x^2\)の係数が負の数であれば上に凸なグラフということが分かります。
これは簡単ですね。
二次関数のグラフの頂点の求め方
二次関数の頂点を求めるには平方完成をします。
・平方完成の仕方は?\(x^2\)に係数があるときや\(x\)の項がない時はどうしたらいいの?
平方完成をして\(y=a(x-p)^2+q\)の形にすれば、二次関数の頂点の座標が分かります。
この形の時の頂点は\( (p,q)\)となります。
「二次関数のグラフが上に凸なのか?下に凸なのか?」、「頂点の座標」の2つが分かれば解の個数を求めることが出来ます。
それでは具体的に例題を解いてみましょう。
<例題>
次の二次方程式の解の個数を求めなさい。
①\(x^2-2x-3=0\)
②\(-x^2+6x-9=0\)
③\(-x^2+2x-3=0\)
①からみていきましょう。
\(y=x^2-2x-3\)と考えます。
まずは上に凸なのか、下に凸なのかからみていきます。
\(x^2\)の係数をみると正の数なので下に凸なグラフと言うことが分かります。
またこの式を平方完成すると\(y=(x-1)^2-4\)となり、頂点の座標は\( (1,-4)\)ということが分かります。
グラフを書きます。
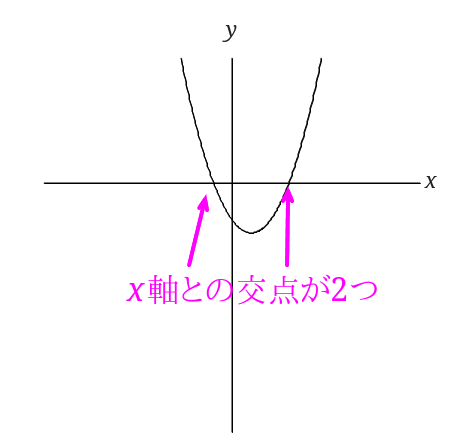
すると\(x\)軸との交点が2つあるので、この方程式は異なる2つの実数解をもつといえます。
②にいきましょう。
\(y=-x^2+6x-9\)と考えます
上に凸なのか、下に凸なのかから考えます。
\(x^2\)の係数が負の数なので上に凸なグラフということが分かります。
この式を平方完成すると\(y=-(x-3)^2\)となるので頂点の座標は\( (3,0)\)となります。
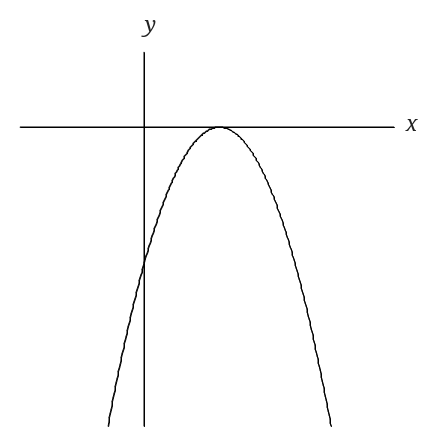
グラフからこの二次方程式はただ1つの実数解(重解)をもつことが分かります。
③にいきましょう。
\(y=-x^2+2x-3\)と考えます。
\(x^2\)の係数が負の数なので上に凸なグラフですね。
次に平方完成をします。
\(y=-(x-1)^2-2\)
となるので、頂点は\( (1,-2)\)となります。
グラフを書きます。
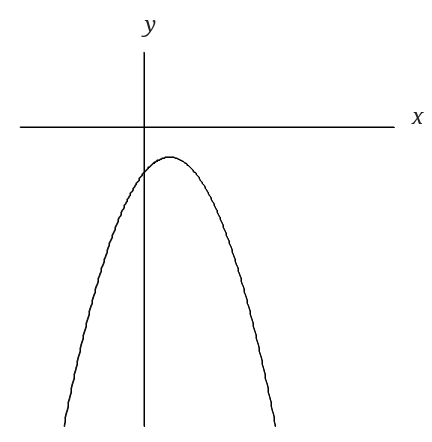
グラフからこの二次方程式は実数解をもたないことが分かります。
まとめ
今回はグラフを書いて二次方程式の解の個数の求める方法をご紹介しました。
判別式を用いれば何も考えずに二次方程式の解の個数を求めることが出来ますが、グラフを書くことで理解が随分と深くなるのではないでしょうか。
実際にグラフを書くのは面倒ですが、二次関数のグラフが書けることで応用問題にも対応しやすくなります。
グラフが書けないとちょっと難しくなるだけで、二次関数や方程式の問題に対応できなくなります。
後々の応用問題などへの対応と思って判別式を使った解法に加えて、グラフからも解の個数が出せるようにしておくといいのではないでしょうか。
今回は二次方程式の解を調べることが目的だったので、グラフを書くときに、どちらに凸なグラフなのかということと頂点の座標のみを使いました。
二次関数のグラフを書くことが目的の場合は\(x\)軸の交点と\(y\)軸の交点まで書き込んでおくことが安心ですよ。




