平行線を利用して同じ面積の三角形を書く時によく使う等積変形。
小学校の三角形の面積の公式をならったときに何となく登場し、中学校の定期考査ではあまり活躍の場がないのですが、これが受験となると使えなくて困ることもあります。
考え方を飲み込むのが大変かもしれませんが分かってくると、なかなか使えます。
結構上位にいる子や数学が得意というのであれば是非マスターしておきましょう。
受験でもよく出てきますしね!
今回は等積変形を使って解く二次関数を扱っていきます。
目次
二次関数の面積の問題を等積変形で解く
等積変形だけでも難しそうなのに、それに関数なんて・・・
と尻込みする必要はありません。
意外とすること自体は簡単です。
そうは言っても数学が苦手な子にはちょっと難しいかもしれません。
数学が苦手なこの場合は等積変形は他の易しい問題ができたら取り組んでもいいかもしれませんね。
逆に数学が得意な子や上位の高校に進学しようと考えている子は必ずできるようにしておきましょう。
受験での関数は全部できるくらいでOKです。
この記事は等積変形そのものが分からないと意味が分かりません。
等積変形そのものが分からないときはこちらのページで勉強してきてくださいね。
やり方を覚えるのも大事ですが、意味をつかんでおくとなぜそうするのかが分かります。
なんとなくは分かるけど理屈が分からないときも是非読んでみてくださいね!
・等積変形で面積が同じ三角形を書こう
それでは、等積変形を使った二次関数の問題をみていきましょう。
二次関数の等積変形を使った解き方
それでは、早速例題をみていきましょう。
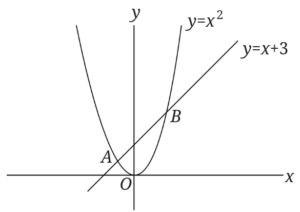
\(\triangle ABO\)の面積と\(\triangle ABP\)の面積がが等しくなるように、放物線上に点\(P\)を取ります。
点\(P\)の座標を全て求めましょう。
もう訳が分からないという人もいるかもしれませんね。
やたら目ったら平行線を書いてはダメですよ。
まずは問題をよく読みましょう。
この時にまず注目するところは、\(\triangle ABO\)の面積と\(\triangle ABP\)の面積がが等しくなるようにというところの三角形をしめした記号です。
\(A\)と\(B\)は共通ですよね。
つまりこの2つの三角形は辺\(AB\)を底辺とみると、この2つの三角形の面積が等しくなるには高さが等しくなればいいということが分かりますよね。
ここから、等積変形が使えるということが判断できますね!
点\(P\)が放物線の\(A\)と\(B\)の間にある時を考えます。
\(AB\)が共通な辺になるので、直線\(AB\)と平行で原点を通る直線を引きます。
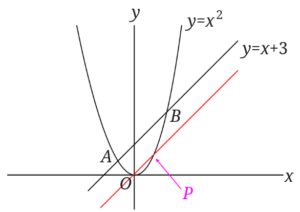
こんな感じになりました。
すると放物線と今引いた直線の交点ができました。
ここが1つ目の\(P\)ということになります。
交点の座標を求めましょう。
先ほど引いた直線は直線\(AB\)に平行な直線なので傾きが\(1\)ということになります。
放物線の式と直線の式で連立方程式を作ります。
\(\begin{eqnarray} \left\{ \begin{array}{l} y=x \\ y=x^2 \end{array} \right.\end{eqnarray}\)
これを解くと\(x=0,1\)となります。
\(x=0\)は原点\(O\)のことなので、点\(P\)が放物線の\(A\)とp\(B\)の間にある時の\(x\)座標が\(1\)なので、点\(P\)の座標は\( (1,1)\)ということになります。
点\(P\)が放物線の\(A\)と\(B\)の外にある時を考えます。
先ほどの書いた直線は直線\(AB\)の下側でしたが同じように上にも同じ面積の三角形作れるはずですよね。
直線\(AB\)と原点を通る直線の距離と同じ距離にある直線を書きましょう。
\(y\)軸を基準に考えると分かりやすいと思います。
直線\(AB\)が\( (0,3)\)を通り、原点を通る直線は\( (0,0)\)を通っているので、直線\(AB\)の上に書く直線は、点\( (0,6)\)を通り傾きが1の直線ということになります。
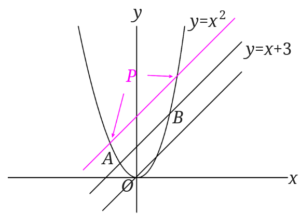
交点が2つできました。
この2つの交点が点\(P\)ということになります。
連立方程式を立てて解いてみましょう。
\(\begin{eqnarray} \left\{ \begin{array}{l} y=x+6 \\ y=x^2 \end{array} \right.\end{eqnarray}\)
これを解くと\(x=-2,3\)となります。
点\(P\)の座標を求めると、\( (-2,4),(3,9)\)ということになります。
よって答えは、(1,1),(-2,4),(3,9)となりました。
この問題の場合は点\(A\)と点\(B\)の間にある点はすんなり出せるのですが、反対側の2点は忘れがちです。
直線\(AB\)と原点を通る直線と同じ距離にある点であれば面積が等しくなることをイメージできれば、反対側の2点も忘れにくくなるのではないでしょうか。
等積変形のコツは?
関数で等積変形を使うのって難しいですよね。
等積変形を使って関数の問題を解こうとすると難しくなります。
問題は関数の問題に見えますが、まずは関数と見ないようにしてみてください。
まずは図形として見るようにしてみましょう。
同じ面積の図を描こうという作図の問題とみるということです。
作図ができれば後は立式するだけです。
計算はしゅっとできるようにしておきましょう。
まとめ
今回は等積変形を使った二次関数の問題を扱ってみました。
問題そのものは難しくないことが多いのですが、考え方を思い浮かべられるかが勝負所ですね。
まずは関数としてではなく、作図の問題として問題を見るようにしましょう。
そうすることで随分考えやすくなるのではないでしょうか。
平行線をきちんと書くことができればあと1歩で問題は解けます。
きちんと式を立てて丁寧に計算をしましょう。




