地味な存在でも実は大事だというものは世の中にはたくさんあります。
素因数分解もそのうちの1つです。
やったからなに？と習いたての頃は見えるかもしれませんが、後々これがないと困ってしまう…
というくらい大切な道具になってくれます。
今回の記事では、素因数分解のやり方について、書いてみたいと思います。
素因数分解って何？
素因数分解という言葉は今までに聞いたことがありますか？
中学受験をしたという子は聞いたことや、やったことがあるかもしれません。
そうでない子の中には初めて聞くという子もいるのではないでしょうか。
素因数分解とは、「ある数を素数の積にすること」です。
まずは素数を知るところからスタートしましょう。
素数って何？
素数ってどんな数でしょうか。
素数とは1とその数の2つしか約数を持たない数をいいます。
約数を2つもつところがポイントですよ。
約数を2つもつものなので、1は素数ではありません。
1は約数を1の1つしか持っていません。
そのため、素数という扱いはされないんですね。
2の約数は1と2の2つだけですね。
そのため2は素数となります。
また3も同じように1と3の2つだけしか約数を持ちません。
そのため3も素数ということになります。
4の約数を考えてみると、1と2と4の3つがあります。
素数は1とその数の2つしか約数を持たないという条件に当てはまらないので、4は素数ではないということになります。
素数は約数を2つしかもたないものと覚えておけば十分だと思います。
また、1は素数ではないということを覚えておくと1を素数と扱ってしまうこともなくなるのではないでしょうか。
連除法(はしご算)を使って素因数分解をやってみよう。
連除法を用いて計算してみましょう。
連除法の別名はすだれ算や逆さ割り算と言われることもあります。
このやり方が最も一般的なやり方になる上に、素因数分解をするときには扱いやすいです。
しっかりマスターしてくださいね。
それでは例題を用いて説明していきます。
1つ1つ順番に説明していきます。
まずは、紙に168と書きましょう。
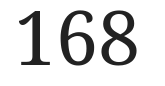次に割り算の筆算の記号をひっくり返した感じの記号を書きます。
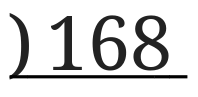
168は偶数なので2で割れるので、先ほど書いた記号の左側に2と書きます。
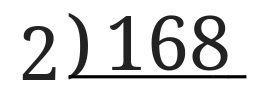
168の下に168を2で割った数、84を168の下に書きます。
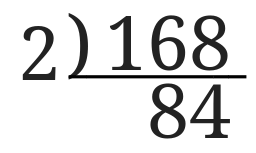
84はまだ割れるので割り算の筆算の記号をさかさまにしたものを書きます。
84は偶数なのでさらに2で割ります。
84の左側に2と書き、84の下には84を2で割った商42を書きます。
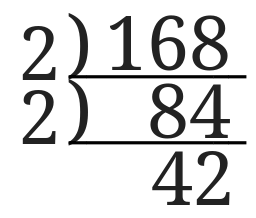
これを商が素数になるところまで続けていきます。
〇で囲んだところが素数になったのでここでおしまいとなります。
で、どうするのかというと、〇で囲んだ数を全部かけると素因数分解の出来上がりです。
168を素因数分解すると、$$168=2\times 2\times 2\times 3\times 7=2^3\times 3\times 7$$となります。
素因数分解をするときにはこの連除法を使うのがとても便利です。
このやり方がおすすめですよ。
もちろん見ただけで素因数分解できるようなものであればそれでもOKですよ。
連除法は見ただけではわからない時に使う筆算のようなものだと考えてもらえればいいと思います。
連除法が面倒だなぁということであれば、少しずつ因数分解していくというのもありです。
168を素因数分解するときに素数ではない数で構わないので、掛け算の式にして少しずつ素数に近づけていくという方法です。
168という数字を見て8で割れることが分かったとすると、まず\(168=8\times 21\)ということがわかります。
さらに8は\(2^3\)、21は\(3\times 7\)ということがわかるので、\(168=2^3\times 3\times 7\)ということが分かります。
パッと見た時に、ある程度大きな数で割れることが分かればこちらの方がはやいのではないでしょうか。
まとめ
今回の記事では、素因数分解のやり方について、書いてみました。
まずは素数の意味をきちんと把握することが大切です。
よく中学生に「素数って何？」と聞くと、「なんだったけ？」となりがちです。
素数は約数を1とその数の2つしか持たないものということをきちんと覚えておきましょう。
中間考査や期末考査などの定期考査で1から20の間の素数を書き出しなさいのような問題を出されたときについ1と書いてしまう子が結構います。
1は素数でないことを覚えておくと引っかからないのではないでしょうか。
素因数分解では基本的には連除法がを使うことがおすすめです。
慣れてきたら、少しずつ小さな数からなる掛け算の形に因数分解をしていくのもいいと思います。
きちんと数がすべて素数になるようにすればOKです。
