分子や分母に分数が入る計算は基本的に小学校や中学校では習いません。
計算問題や文章問題でも分数の分子や分母に分数がある式[1]\(\frac{\frac{2}{3}}{\frac{5}{7}}\)のような分数は繁分数(「はんぶんすう」と読みます。)と呼ばれます。になってしまうこともあるのではないでしょうか。
しかし、学校では習っていないとはいえ、計算の途中で出てきてしまうこともあります。
この記事では分数の分子や分母が分数になってしまうときの計算方法について書いてみたいと思います。
分数の中に分数がある繁分数の計算方法って?
よほどの難関高校の受験を考えている子でなければ、基本的に分数の分子や分母に分数が入った計算は出題されることはありません。
入試などで問題として出題されなくても、計算の途中に分数の分母や分子が分数になってしまう場合があります。
分数の分母や分子に分数が入ってしまうと、「計算できませーん・・・」となってしまいがちです。
ちょっとした計算ができれば答えを出せるのに勿体ないです。
小学校や中学校の算数や数学で習う範囲で、この場合になることがある最も身近な例が中学1年生の反比例の問題なので、分数の分子や分母に分数が入った計算を避けてうまく計算する方法を反比例の例題を使って説明します。
(1)\(x=2\)のとき、\(y\)の値を求めなさい。
(2)\(x=\frac{5}{3}\)のとき、\(y\)の値を求めなさい。
反比例の問題です。
それでは(1)からみていきます。
\(x=2\)のときの\(y\)の値を求めればいいので、\(x\)に2を代入して計算します。
すると\(y=\frac{12}{2}=6\)となり、答えは\(y=6\)となります。
これは代入すればいいだけなのでなんてことないですね。
次に(2)をみてみましょう。
\(x=\frac{5}{3}\)を\(y=\frac{12}{x}\)に代入します。$$y=\frac{12}{\frac{5}{3}}$$という形になってしまい、どうすればいいのかさっぱりとなってしまいます。
割り算の性質を使って、分数の上や下に分数が入らないようにして計算しよう
まずは、この計算をみてくださいね。$$1\div2=\frac{1}{2}$$となるのは、中学生にはそんなに難しい計算ではないと思います。
この計算の逆を利用して、分数の分子や分母に分数を入れることなく計算してみます。
つまり、\(〇\div △=\frac{〇}{△}\)の逆、\(\frac{〇}{△}=〇\div △\)を利用します。
先程の\(\frac{〇}{△}=〇\div △\)を利用して、\(y=\frac{12}{x}\)を変形すると、\(y=12\div x\)とすることができます。
ここに\(x=\frac{5}{3}\)を代入して計算すると、$$y=12\div \frac{5}{3}$$となり答えは\(y=\frac{36}{5}\)となります。
割り算の考え方をきちんと使うことができると、今までに学校で習った範囲で計算できました。
繁分数にして計算すると
先ほどの解き方では、\(\frac{12}{x}\)を\(12\div x\)にして計算しました。
今度は、分数の状態のまま\(x\)に\(\frac{5}{3}\)を代入してみます。$$y=\frac{12}{\frac{5}{3}}$$となります。
分母の分数の分母が邪魔なので、分母と分子に3を掛けてみます。[2] … Continue reading$$y=\frac{12\times 3}{\frac{5}{3}\times 3}$$となります。
後は計算してみると。
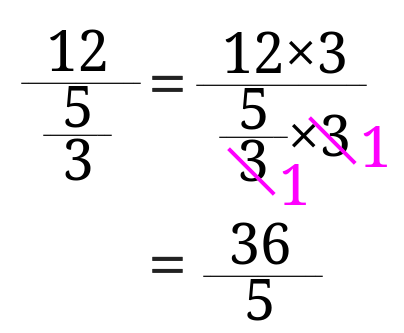
答えは、\(y=\frac{36}{5}\)となります。
小学校や中学校ではこの解き方は避けた方がいいかも
勿論この解き方でも問題ないのですが、中間考査や期末考査のような定期考査では注意が必要な時があります。
この問題で途中式まで書かないといけない時に、学校で教えていないという理由で、正解として扱ってもらえないことがあるので気をつけましょう。
中学校のワークでは、\(y=\frac{a}{x}\)を\(y=a\div x\)に変形して\(x\)に分数の値を代入するという解法が一般的です。
そのため前者の\(\frac{12}{x}=12\div x\)として計算するのが公立中学では一般的です。
繁分数の計算の仕方を中学校の先生から習っているときは良いのですが、そうでない時は定期考査前に先生に尋ねておいた方が安心ですよ。
まとめ
今回の記事では、分数の分子や分母が分数になってしまう時の計算の仕方について書いてみました。
公立中学校では、計算途中で繁分数になってしまうというのは、反比例の\(x\)に分数を代入するときくらいでしょうか。
そんなに出会う機会が多い計算式ではないので、数学が苦手だとどうしていいのか戸惑ってしまうこともあると思います。
基本的には、\(\frac{〇}{△}=〇\div △\)のように、分数を割り算の式に直して代入すればいつも通りに計算することができます。
数学が得意な子であれば、繁分数の計算の仕方までできるようになっておくといいと思います。
中学校のテストでは、習っていないから不正解ということがあるので、繁分数はあまり見せたり、書かたりしないほうがいいかもしれません。
答案で計算式を見られてしまうという時は、分数を割り算の式にして計算したように見せるか、割り算の式にして計算するようにするといいです。




