平行線を使うと面積が同じ三角形をたくさん書くことが出来る等積変形。
理屈は分かってもどう使うべきか分かりにくいところもあります。
初めて見た問題だとどう等積変形を使えばいいのか分からないこともあるのではないでしょうか。
今回の記事では等積変形の応用問題を扱ってみたいと思います。
等積変形を使って作図してみよう。
等積変形を使って面積を変えずに別の図形にする作図は中間考査や期末考査のような定期考査ではよく見かけるのではないでしょうか。
定期考査を除くと急に作図の存在感は薄れてしまいますが、知識そのものは受験でも問われることがあります。
色々な図形を等積変形を使って面積をそのままに別の図形に書き換えてみましょう。
この記事では、
・五角形→三角形
・五角形→四角形
・境界線をまっすぐな直線に書き換える等積変形
を扱っていきます。
それでは等積変形を使って、五角形を三角形にする作図からみていきますよ。
等積変形を使って五角形を三角形にしてみよう
＜例題＞
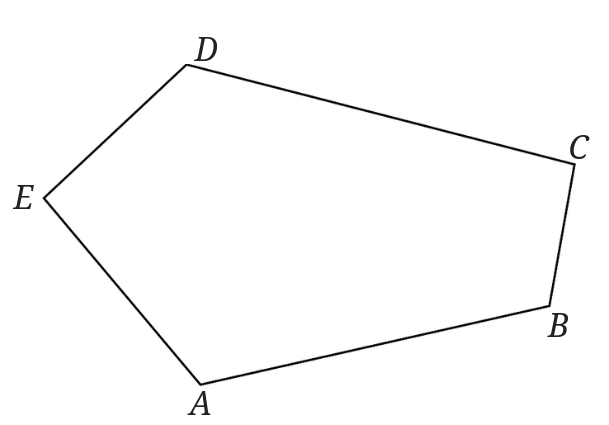
適当な形の五角形を面積をそのままで三角形にしてみましょう。
直線\(AB\)上に二つの点、\(F\)と点\(G\)をとり\(\triangle AFG\)を作ってみます。
まずは直線\(AB\)を書き込んでみましょう。
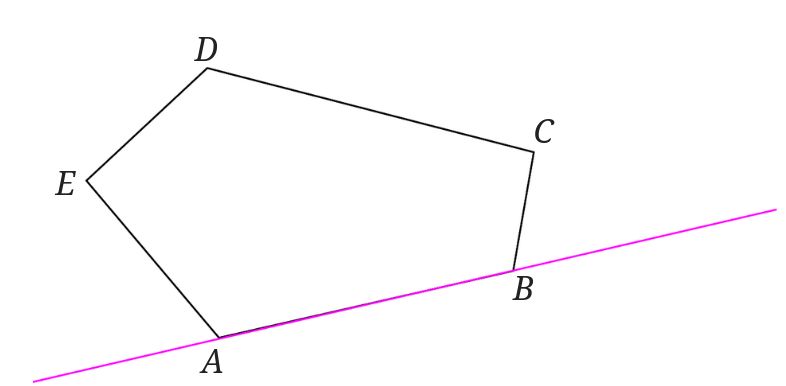
次に対角線を書きます。
点\(A\)と点\(D\)を、点\(B\)と点\(D\)を結びます。
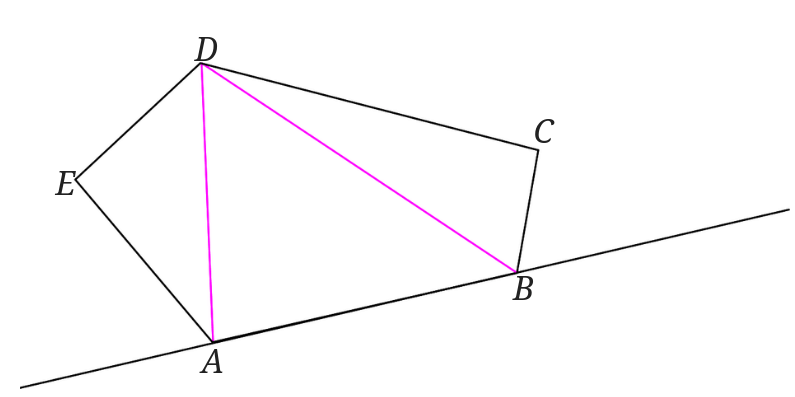
点\(E\)を通り直線\(AD\)に平行な直線\(l\)を引きます。
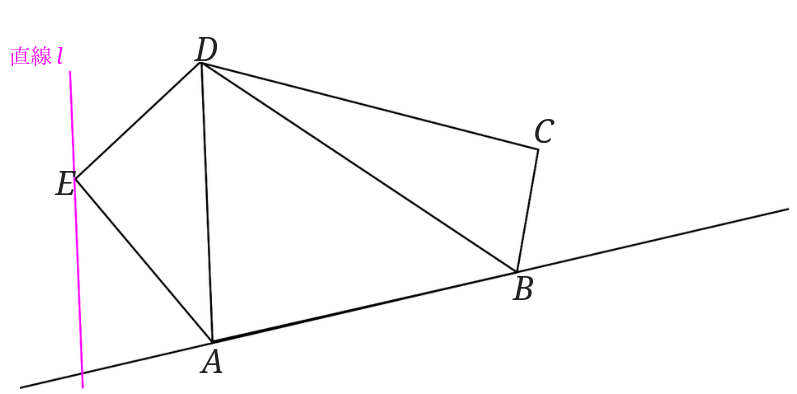
直線\(l\)と直線\(AB\)の交点と点\(D\)を結びます。
またその交点を\(F\)とします。
同じように点\(C\)を通り直線\(BD\)に平行な直線\(m\)を引きます。
直線\(m\)と直線\(AB\)の交点を\(G\)とします。
点\(D\)と点\(G\)を結びます。
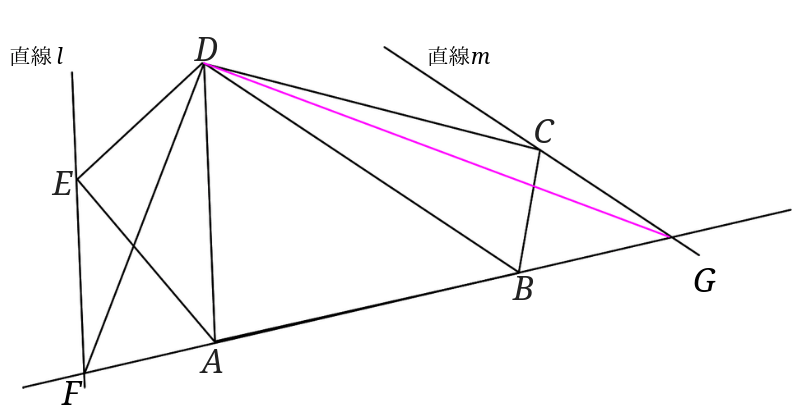
これで五角形\(ABCDE\)を面積を変えることなく\(\triangle FDG\)に書き換えることができました。
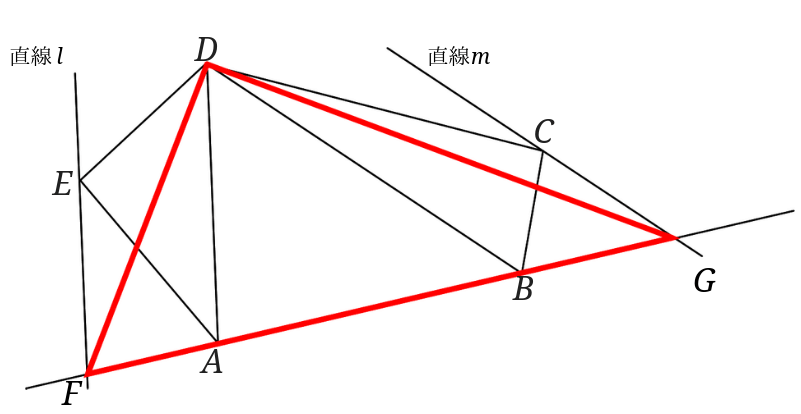
五角形そのものを等積変形で別の図形に書き換えることができないため、三角形に分解するのがポイントですね！
等積変形を使って五角形を四角形にしてみよう
五角形を四角形に書き換えてみましょう。
＜例題＞
次の五角形\(ABCD\)を四角形\(ABCP\)に書き換えましょう。
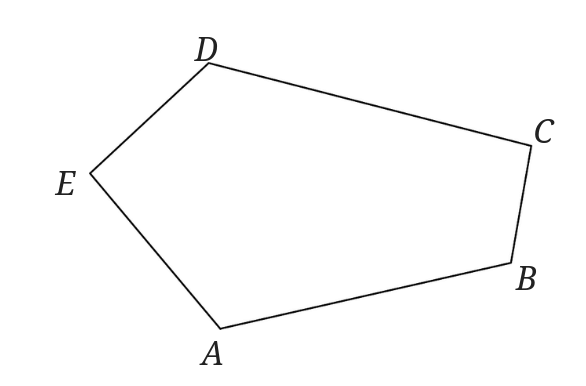
ちょっと考えないと難しいですね。
まず点\(E\)と点\(C\)を結びます。
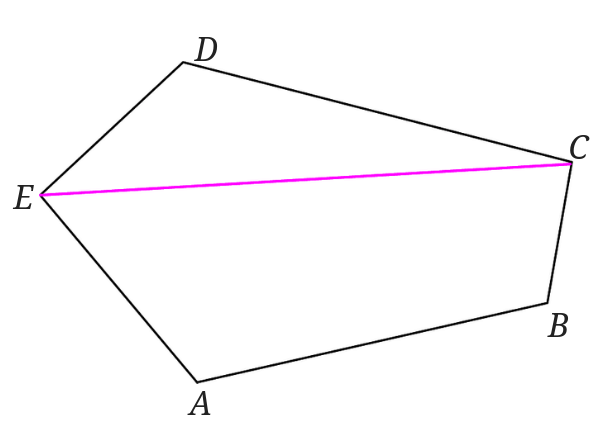
点\(D\)を通り直線\(EC\)に平行な直線\(m\)を引きます。
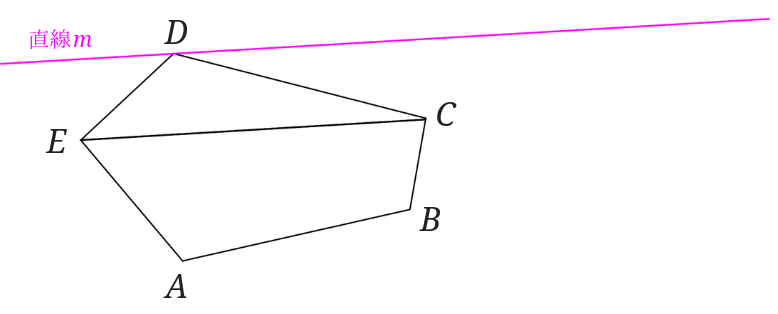
直線\(AE\)を伸ばして、直線\(m\)との交点を\(P\)とします。
あとは点\(P\)と点\(C\)を結んで四角形\(ABCP\)で出来上がりです。
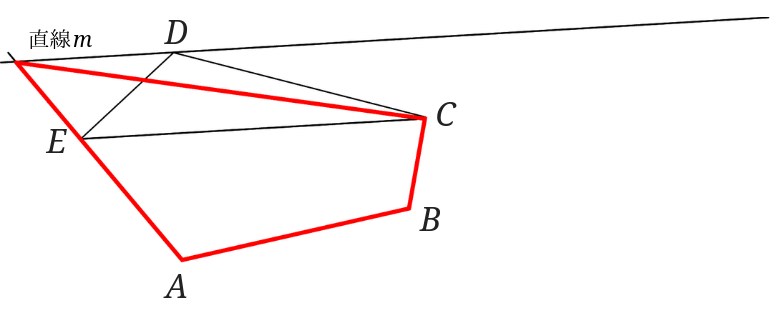
直線\(AE\)上に点\(P\)を取るのがポイントです。
等積変形は平面図形では三角形と平行線をもとに同じ面積の三角形がかけるというものです。
どの三角形をもとに面積が同じ三角形をどこに作るのかを考えられるといいですね。
そこが見えると易しい等積変形の問題と同じようになりますよ。
等積変形を使って境界線をまっすぐにしよう
＜例題＞
下の図形のアの部分の面積とイの部分の面積を変えずに点\(P\)を通る直線で2つに分けましょう。
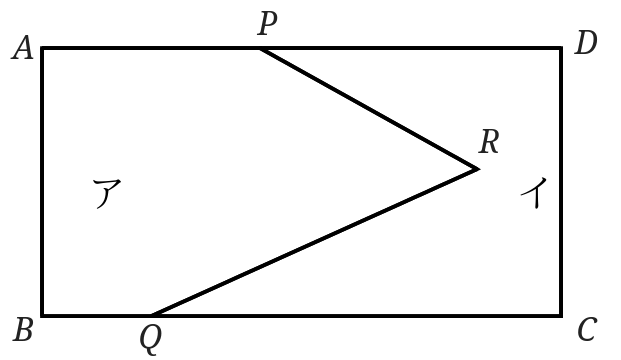
よく見る境界線の問題です。
先程の問題では五角形を三角形にするときに、三角形をうまく作って等積変形を利用しました。
この問題でも同じように三角形を作ってそれを等積変形していきます。
まず点\(P\)と点\(Q\)を結びます。
次に点\(R\)を通り直線\(PQ\)を通る直線を引き、交点を\(S\)と\(T\)とします。
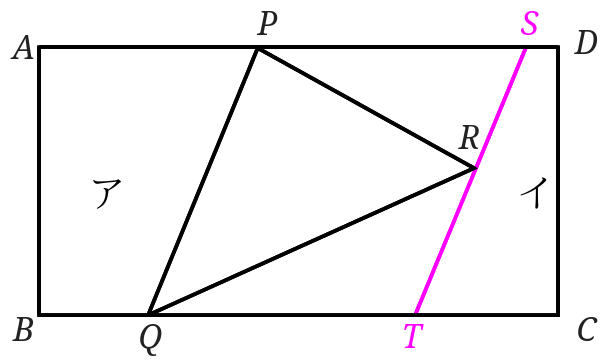点\(P\)を通る直線で面積を変えずに2つに分けるので点\(P\)と点\(T\)と結んで出来上がりです。
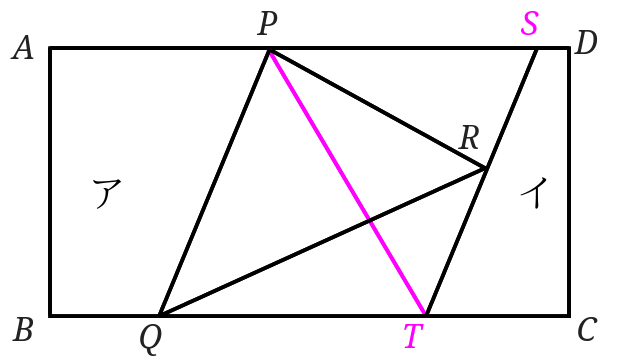
この問題が点\(Q\)を通る直線で2つに分ける場合は、点\(S\)と点\(Q\)を結べばＯＫです。
まとめ
今回は等積変形を使って面積を変えることなく別の図形に書き換える仕方をしてみました。
今回扱ったのは中間考査や期末考査などの定期考査でよく見かける問題です。
自力でできない場合は何度も作図してみて、できるようにしておきましょう。
定期考査ではこれくらいの作図が出来ていればばっちりだと思いますよ。
定期考査ではなく、入試になると作図なんていらないやー！って思う子も多いと思います。
入試で直接作図をさせられることは少ないのは事実です。
しかし、作図の知識などを問われないかというとそんなことはありません。
受験では関数や平面図形、空間図形で等積変形などの作図の知識を使うことがあります。
作図なんて出ないやと思わずに作図もできるようにしたおくことがおすすめです。
ちょっと難しいと思っても作図はきちんとできるようにしておきましょう。
