ルートの中が分数の時の掛け算の計算の仕方のコツって？

ルートのついた計算は慣れるまでは混乱しやすいものです。

ただちょっとしたコツで簡単になったり難しくなったりしてしまいます。

今回の記事では、分数のルートの計算のコツについて書いてみたいと思います。

ルートの掛け算の計算で分数がある時のコツ

それでは早速例題をみていきましょう。

(1)\(\sqrt{\frac{2}{3}}\times \sqrt{\frac{5}{7}}\)からみていきます。
ルートのついた数の同士の掛け算は、普通の分数の掛け算と同じように、分子は分子同士、分母は分母同士掛けることで計算することができます。

(1)\(\sqrt{\frac{2}{3}}\times \sqrt{\frac{5}{7}}\)
\(=\sqrt{\frac{2\times 5}{3\times 7}}\)
\(=\sqrt{\frac{10}{21}}\)

\(\frac{2}{3}\times \frac{5}{7}\)の計算と同じように計算することができました。
あとは分母を有理化して、答えは\(\frac{\sqrt{210}}{21}\)となります。
勿論先に有理化して計算してしまってもOKです。
次に約分ができるタイプの計算をみてみましょう。

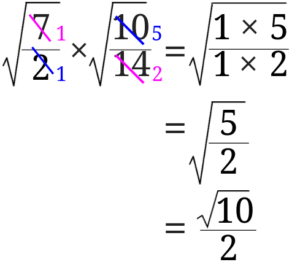
今までの分数の計算と同じように途中で約分をすることが可能です。
約分を途中でしないとルートのなかの数が大きくなってしまい、約分ができることに気付けなくなりがちです。
また、約分ができることに気付かないと、分母を有理化したときに分子の数がとんでもなく大きくなりがちです。
そうなると、ルートの外に数字をくくりだすのに一苦労…ということにもなりかねません。
計算が苦手な子の場合、ここで手が止まってしまうということは少なくないのではないでしょうか。
約分ができるときは先に約分をして、ルートの中の数をより小さくしておくと計算が楽になります。
・ルートの掛け算の計算の仕方のコツって？

次に整数掛けるルートのついた分数の計算をしてみましょう。
(3)\(3\times \sqrt{\frac{2}{3}}\)
この場合も今までのルートのついていない分数の計算と同じです。
\(=\frac{3\times \sqrt{2}}{\sqrt{3}}\)
\(=\frac{3\sqrt{2}}{\sqrt{3}}\)
後は分母を有理化して、
\(=\sqrt{6}\)
となります。

先に分母を有理化してしまって、
\(3\times \frac{\sqrt{6}}{3}\)
として、約分してしまうという順番でもいいと思います。
約分が先か有理化が先かでは、約分ができるようであれば約分を先にしたほうが計算が楽になることが多いです。
（ルートが完全に外れてしまって、整数になるような場合はルートを先に外してしまったほうが楽になります。）
この辺りは計算の好みもあるので、得意なやり方でするのがいいと思います。

まとめ

今回の記事では、分数にルートがついた掛け算の計算方法について書いてみました。
計算の仕方は、ルートのついていない分数の計算方法と同じように計算することができます。
公式として覚えてしまうというよりは、ある程度計算をして慣れてしまえば、大丈夫という子が多い計算です。
どのように数字をさわればいいのか、まずは慣れるようにするといいと思います。

ルートのついた分数の計算では約分や分母の有理化などすることが多いので、計算でどうしても混乱してしまうということもあると思います。
そんな時は、まずは分数でないルートのついた掛け算からやってみることがおすすめです。
分数でないルートの計算に慣れたてからルートのついた分数の計算に取り掛かるとスムーズに学習することができると思いますよ。