因数分解を使って二次方程式が解けない時に使うのが解の公式。
今まで出てきた公式のどの公式よりもややこしそうに見えます。
今回の記事では解の公式を使った二次方程式の解き方を紹介します。
中学校で習う解の公式を使った二次方程式の解き方
二次方程式を解の公式使って解いてみましょう。
(1)\(3x^2-7x+1=0\)
(2)\(4x^2+3x-1=0\)
(3)\(2x^2-4x-3=0\)
まずは解の公式を覚えてくださいね。
二次方程式\(ax^2+bx+c=0\)である時$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
\(a\)は\(x^2\)の係数、\(b\)は\(x\)の係数、\(c\)は定数項の部分になります。
(1)\(3x^2-7x+1=0\)であれば、\(a=3\)、\(b=-7\)[1]マイナスの符号をつけ忘れてしまう子がいるので注意しましょう。、\(c=1\)ということになります。[2]右辺の数が0になっていないと解の公式は使えません。解の公式を使って解くときは、すべての項を左辺に移項して右辺を0にしてください。
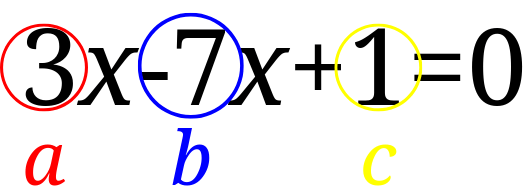 解の公式を実際に使って、(1)\(3x^2-7x+1=0\)を解きましょう。
解の公式を実際に使って、(1)\(3x^2-7x+1=0\)を解きましょう。
\(a=3\)、\(b=-7\)、\(c=1\)を解の公式に代入しましょう。
・因数分解を利用した二次方程式の解き方のコツは?
\(x=\frac{-(-7)\pm \sqrt{(-7)^2-4\times 3\times 1}}{2\times 3}\)
\(x=\frac{7\pm \sqrt{49-12}}{6}\)
\(x=\frac{7\pm \sqrt{37}}{6}\)
このように解の公式は単に代入するだけで、解を求めることができます。
この問題では、ルートの中身を小さくすることができなかったので、そんなに手間はありませんでした。
しかし、ルートの中身を小さくするなどという手順が必要な場合はミスが増えやすいです。
よくあるミスをしやすい問題を(2)、(3)で用意しました。
解の公式を使って解いたときに多いミスを知ってミスを減らそう
それでは、(2)\(4x^2+3x-1=0\)を解いてみましょう。
解の公式に代入します。[3]この問いでは、\(a=4\)、\(b=3\)、\(c=-1\)となります。
\(x=\frac{-3\pm \sqrt{3^2-4\times 4\times (-1)}}{2\times 4}\)
\(x=\frac{-3\pm \sqrt{9+16}}{8}\)
\(x=\frac{-3\pm \sqrt{25}}{8}\)
\(x=\frac{-3\pm 5}{8}\)
見かけるのがここで計算を止めてしまう子です。[4]ルートを外し忘れる、もしくはルートの中の数を小さくするのを忘れてしまうこも結構います。
計算できるときは、きちんとできるところまで計算するようにしましょう。
さらに計算すると
\(x=\frac{2}{8},\frac{-8}{8}\)[5]ここでも約分を忘れないように
\(x=\frac{1}{4},-1\)
ここまで計算出来たら正解です。
途中で計算を止めないようにできるといいですね。
さらに(3)を見ていきましょう。
(3)\(2x^2-4x-3=0\)[6]この問いでは、\(a=2\)、\(b=-4\)、\(c=-3\)となります。を解きます。
\(x=\frac{-(-4)\pm \sqrt{(-4)^2-4\times 2\times (-3)}}{2\times 2}\)
\(x=\frac{4\pm \sqrt{16+24}}{4}\)
\(x=\frac{4\pm \sqrt{40}}{4}\)
\(x=\frac{4\pm 2\sqrt{10}}{4}\)
ルートの中もこれ以上小さくできないので、答えが出せたと思いがちですが、あと一歩というところです。
この時は約分ができるので、約分までしてはじめて正解となります。
答えは、\(x=\frac{2\pm \sqrt{10}}{2}\)となります。
・「できる子」は知っている二次方程式を因数分解すると解が導ける理由
まとめ
今回の記事では解の公式を使った二次方程式の解き方を紹介します。
解の公式は中学生の目から見るとかなりややこしい公式です。
また見た目がややこしいだけでなく、ルートの扱いに慣れていない子や、分子が複数の項ある分数の約分ができない子にとっては、難しい計算になります。
二次方程式の解の公式の練習をする際には、そういった細かいところまでできるようにするといいと思います。
そもそも解の公式が中学生にとっては複雑に感じる公式なので、慣れるための練習は不可欠です。
スラスラ迷いなく解の公式が使えるというところまでしておくことがおすすめです。




