平方根の求め方って？分数や小数の時はどうしたら良いの？

2乗するとある数になる数を、ある数の平方根といいます。

例えば1の平方根はいくらですか？

と、聞かれれば1と-1と答えるとOKです。

4の平方根はいくらですか？

と、聞かれれば2と-2と答えられると思います。

ただこの数が大きくなってきたり、分数や小数のように少し難しくなると同時にミスも増えやすくなってしまいます。

今回の記事では、平方根の求め方について考えてみたいと思います。

平方根の求め方

それでは早速例題を使いながら考えてみます。

数字が小さいので、見ただけで分かる！となってしまうと思いますが、4の平方根を求めてみましょう。
平方根を求めるには素因数分解を使いますよ。
・素因数分解の意味や書き方がわからない！連除法（はしご算）を使った簡単なやり方を解説！

4を素因数分解すると、\(4=2^2\)となります。
連除法を使って4を素因数分解するとこんな感じになります。

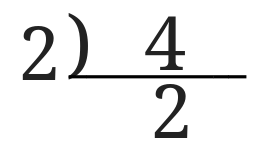
よって、4の平方根は2ということになります。
と、いう感じで答えを書くとバツとなってしまいます。
平方根を答えなさいと言われたら、必ず正の数と負の数があると考えておきましょう。^[1]例外は1つあり、それは0です。0の平方根はいくらかと聞かれたら、0でOKです。\(\pm0)と書かないように注意しましょう。
4の平方根は、+2と-2となります。
ただこのまま書くと面倒なので、\(\pm2\)と書けばOKです。

4くらいなら見れば分かる！と言われそうなのでもう少し大きな数を見てみましょう。

ずいぶん大きくなりました。
平方根を答える問題では、基本は素因数分解です。
それでは144を素因数分解してみましょう。
連除法を用いて素因数分解数するとこんな感じになります。

\(144=2^4\times 3^2\)となります。
少し式をいじってみると、\( (2^2\times 3)\times (2^2\times 3)=(2^2\times 3)^2=12^2\)となりました。
よって144の平方根は、\(\pm12\)ということになります。
そんなに難しくはありませんね。
きちんとまずは素因数分解ができるようにしましょう。

さらに分数や小数の平方根についてみていきましょう。

分数の平方根を求めよう。

分数を見ただけでイヤー！という子は結構いると思いますが、実は平方根ではかなり扱いやすいです。
見た目で食わず嫌いにならずに分数の平方根を求めてみましょう。
例題を見ていきましょう。

分数だと見た目は難しくなりますが、意外と平方根を求めるのはやりやすいです。
これはなぜかというと分母と分子を別々に考えて平方根を求めればいいからです。
\(\frac{4}{9}\)の平方根を考えるとき、分子の4と分母の9を別々に考えればいいということです。
分子の4は\(2^2\)、分母の9は\(3^2\)です。
つまり、\(\frac{4}{9}\)の平方根は、\(\pm\frac{2}{3}\)ということになります。

分数は分子と分母を別々に扱って平方根を求めることができるので、意外とやりやすいものです。
それと比べると、小数はちょっと扱いにくくなります。

小数の平方根を求めよう。

小数の平方根って意外と間違う子が多いものです。
そのまますると、なんだかミスが多いなぁという子やうまく平方根を見つけることができないというときはちょっとやり方を工夫すると楽になります。
それでは例題をみていきますよ。

分かる子にはなんてことのない問題ですが、意外とミスが多い問題でもあります。
0.36の平方根はいくらでしょうか。
まずは自分自身で考えてみてくださいね。

0.36の平方根はいくらか聞かれると、\(\pm0.06\)という答えちゃう子がいます。
これは間違いですよ。
\(\pm0.06\)を2乗すると0.0036となり、2乗しても0.36になりませんね。
小数点以下の桁が増えると扱いにくくもなります。
0.36の平方根は\(\pm0.6\)ですが、ミスが出やすくなりがちです。
そんなときは分数にして考えてみましょう。

小数は分数にして平方根を考えると楽？！

0.36を分数にすると\(\frac{36}{100}\)となります。
分数の平方根は分子と分母を別々に考えて求めることができます。
分子の36は\(6^2\)、分母の100は\(10^2\)となります。
0.36の平方根は\(\pm\frac{6}{10}\)と分かります。
あとは約分をして、\(\pm\frac{3}{5}\)と答えればばっちりですね。
きちんと約分するのを忘れないようにしましょう。

また小数を分数にしたときに、分母と分子は約分しないほうが扱いやすいことが多いです。
分母は必ず10の\(n\)乗という形になります。
約分をすると、分母の数がややこしくなるので、分数にしたときには基本的に約分しないのがおすすめですよ。

まとめ

今回の記事では、平方根の求め方について考えてみました。
基本は素因数分解になるので、素因数分解はきちんとできるようにしておきましょう。
また分数の平方根を考えるときは分子と分母の数を別々に考えて平方根を求めることができます。
この方法をうまく使うと、小数の平方根も求めやすくなるのでおすすめですよ。
・平方根の近似値を求めるにはどんな考え方をするの？語呂合わせを使った覚え方は？