2乗すると2になる数を√2、2乗すると3になる数を√3という風に書きます。
きっちりと小数では書ききれない数なので、とても便利なものです。
しかし、√2や√3という数は一体どれくらいの数なのでしょうか。
今回の記事では、平方根の近似値の求め方について書いてみたいと思います。
平方根の近似値の求め方って?
平方根の近似値を求めるには、どうすればいいのでしょうか。
\(\sqrt{2}\)の近似値を求めてみましょう。
まずは\(\sqrt{2}\)の整数部分[1]整数の部分のことです。例えば13.225という数があったとすると、この整数部分は13、小数部分は0.225と言うことになります。を考えてみたいと思います。
数直線を用意してみました。
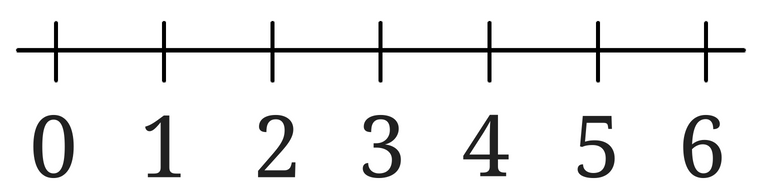
\(\sqrt{2}\)が数直線のどこにあるのかが分かれば、\(\sqrt{2}\)の整数部分が分かります。
ただ、\(\sqrt{2}\)をどうこういじって、分かるものではないので、2乗すると√(根号)がはずれるとう性質をうまく使って考えてみたいと思います。
数直線に書き込んだ数もそれぞれ2乗してみましょう。
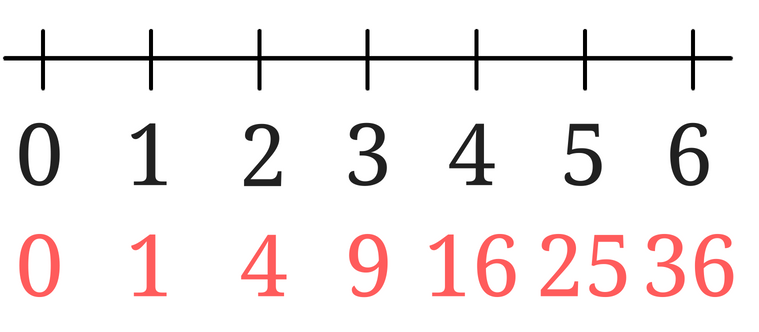
\(\sqrt{2}\)を2乗すると2となります。
と言うことは、\(\sqrt{2}\)は、1と2の間にあることが分かりました。
\(\sqrt{2}\)が、1と2の間にある数と言うことは、\(\sqrt{2}=1.\cdots\)と言うことが分かります。
さらに小数第1位を求めてみましょう。
数直線の1と2の間を拡大してみます。
見にくかったので数字を上下に書いてみました。
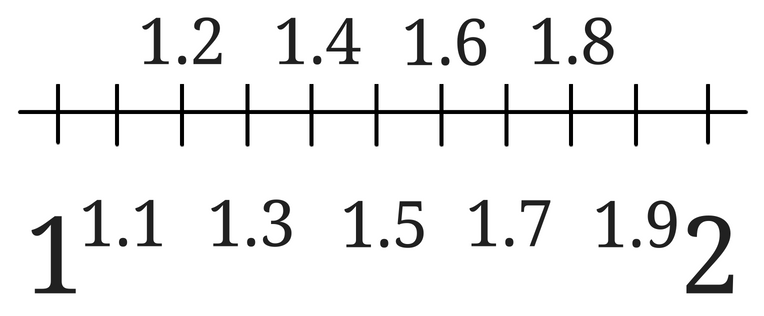
先ほどと同じように数直線上の数を2乗してみます。
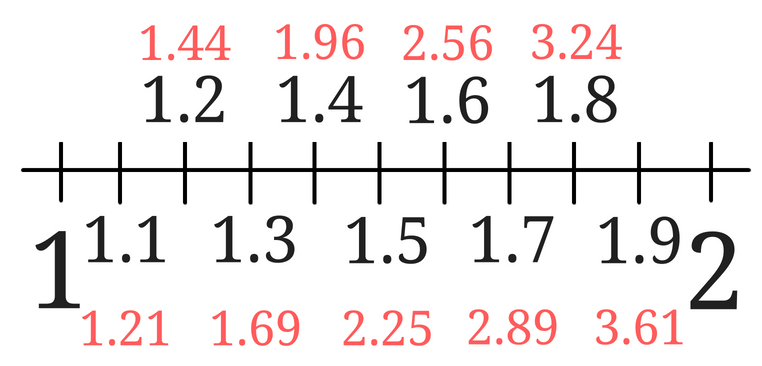
すると2は、1.4と1.5の間にある数ということが分かるので、\(\sqrt{2}=1.4\cdots\)となることが分かります。
さらに小数第二位を求めると、1.41と1.42の間にあることが分かります。
これを繰り返していくと、\(\sqrt{2}\)の近似値をどんどん求めていくことができます。
必要なところまで、ゴリゴリ計算していくと求められることになります。
\(\sqrt{5}\)の近似値を求めてみよう!
同じようにして\(\sqrt{5}\)を求めてみましょう。
数直線で見ると、2と3の間にあることが分かります。
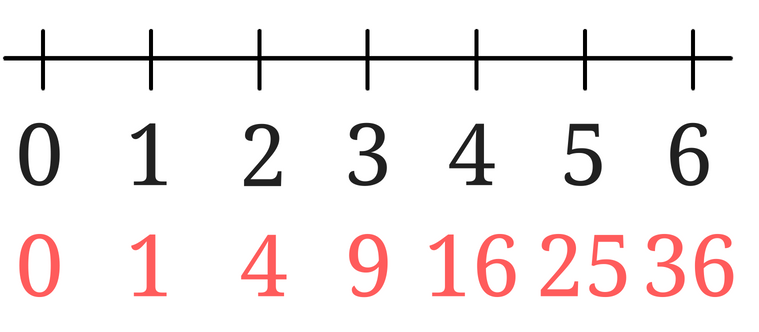
このことから\(\sqrt{5}\)の1桁目は2ということが分かりました。
さらにもう一桁求めてみましょう。
数直線の2と3の間を確認してみますね。
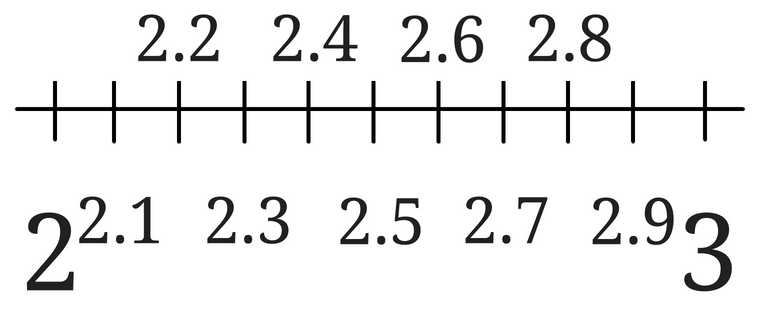
さらにそれぞれの数を2乗してみます。

\(\sqrt{5}\)は、2.2と2.3の間にあることが分かります。
\(\sqrt{5}\)の小数第一位の数は2ということが分かり、\(\sqrt{5}=2.2\cdots\)となります。
数直線上では全ての小数の2乗をとりましたが、実際には大体この辺かなぁと予想を立てて必要なところだけを2乗するという形でOKです。
計算が大変にはなりますが、根性で平方根の近似値は求められますね。
あまり計算はしたくないですが・・・
テスト中にすると時間が足りなくなる?
この方法の問題点は、とにかく時間がかかる点にあります。
桁数が増えれば増えるほど、どんどん計算量が増えていきます。
時間がかかってしょうがないですよね。
中間考査や期末考査のような定期考査で、近似値を求める問題が出たらどうしたらいいのでしょうか。
そんなときのために、\(\sqrt{2}\)や\(\sqrt{3}\)や\(\sqrt{5}\)の近似値を覚えてしまうというのも手です。
平方根の近似値の覚え方は?
\(\sqrt{2}=1.41421356\cdots\)
覚え方は、「ひとよひとよにひとみごろ」と覚えるといいですね。
\(\sqrt{3}=1.7320508\cdots\)
覚え方は、「ひとなみにおごれや」と覚えましょう。
\(\sqrt{5}=2.2360679\cdots\)
覚え方は、「ふじさんろくおうむなく」と覚えましょう。
覚えておくといいかなぁと思われる、平方根の近似値と語呂合わせです。
ただ、覚えたからと言ってそんなに役に立つものでもない気がします。
大体整数部分くらいが分かれば問題を解くときには困らないので、整数部分はどんな平方根を聞かれてもシュッと答えられるようにしておくと言いと思います。
まとめ
今回の記事では、平方根の近似値の求め方について書いてみました。
求め方そのものは、そんなにややこしいものでもないので、すんなりできるのではないでしょうか。
ただ、やり方が分かったところで、する計算はそんなに易しい感じはありません。
桁が増えれば増えるほど大変な計算になっていってしまいます。
そうは言っても、近似値を求めなさいという問題は、そうそう出るものではありません。
一応学校のワークなどで出題があったとしても、電卓マークがついていると思います。
さすがに、この計算を手で計算して解くのは大変です。
定期考査などで出題されてしまった時は後回しにしたほうが賢明かもしれませんね。
References
| ↑1 | 整数の部分のことです。例えば13.225という数があったとすると、この整数部分は13、小数部分は0.225と言うことになります。 |
|---|




