共通因数でくくるというのは因数分解の基礎ではありますが、意外とその共通因数でくくるということが分かりにくい場合もあります。
そんな時は、共通因数を同じ文字で置き換えてから、その文字でくくるというのが定石となります。
文字で置いても分かりにくいてという場合におすすめなのが、「くくる」という考え方ではなく、「足す」という考え方です。
結果は同じになるのですがちょっと風景が変わるのが面白いです。
今回の記事では、共通因数でくくるのが分かりにくい因数分解をするときや、共通因数でくくるのが苦手という子におすすめの方法について書いてみたいと思います。
共通因数でくくるというのは因数分解の基本と言われるけれど･･･
単純な問題であればそんなに共通因数でくくるということは難しいものではないのですが、その形がちょっと複雑になるとどうくくればいいのか分からなくなることもあります。
そんなときにちょっと見方を変えると、共通因数でくくることができるようになります。
例題を使ってみていきましょう。
(1)\(3x+3y\)
(2)\(a(x+y)+(b+c)(x+y)\)
(1)\(3x+3y\)からみていきましょう。
3が共通因数なので、3でくくります。
イメージとしてはこんな感じでしょうか。
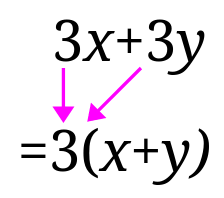3を前にくくりだすイメージでしている子が多いと思います。
ここで少し見方を変えてみると、今までくくりだすという考え方をしていたのが、コロッと変わってしまいます。
掛け算の理屈をもとに考えてみる
小学2年生の時に習った掛け算の理屈をもとに考えてみましょう。
掛け算の理屈とは、例えば、\(2\times 3\)の意味は、「2が3個」もしくは「3が2個」ということです。
この理屈で因数分解をしてみましょう。
先ほどの(1)\(3x+3y\)をその考え方でみてみます。
\(3x\)の意味を「3が\(x\)個」、\(3y\)の意味を「3が\(y\)個」と考えます。
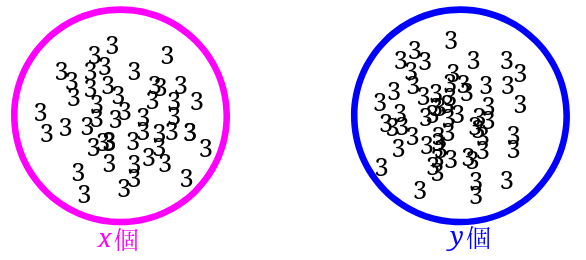すると、\(3x+3y\)の式の意味は、3が\(x\)個と3が\(y\)個あるとき全部でいくらかという感じに見えます。
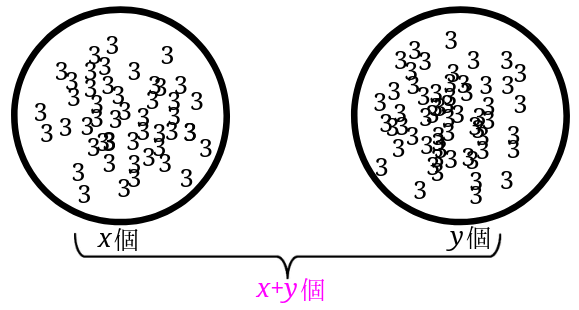全部で3が\(x+y\)個あるので、\(3(x+y)\)となります。
同じようにして、(2)\(a(x+y)+(b+c)(x+y)\)を解いてみましょう。
この問題は、\(x+y\)が共通因数なので、\(x+y=A\)とおいて共通因数でくくる形で解くことが多いと思います。
実際にしてみると、
(2)\(a(x+y)+(b+c)(x+y)\)
\(=aA+(b+c)A\)
\(=A(a+b+c)\)
\(=(x+y)(a+b+c)\)
という、感じになると思います。
\(A\)でくくるところが難しいという子が結構います。
\(aA+(b+c)A\)を掛け算の理屈でかんがえてみると、最初の項\(aA\)は、「\(A\)がa個」という意味です。
また後の項\( (b+c)A\)は、「\(A\)が\(b+c\)個」という意味です。
これらを足すと、\(A\)が\(a+b+c\)個ということになります。
つまり、\(A(a+b+c)\)ということですね。
あとは\(A\)を元に戻して、\( (x+y)(a+b+c)\)となります。
また、\(A\)でおくのも面倒だというときは、初めの式の段階で、\(x+y\)を\(a\)個と\(b+c\)個をあわせると解釈すれば、全体で\(x+y\)が\(a+b+c\)個ということが分かります。
\(x+y\)が\(a+b+c\)個あるということは、\( (x+y)(a+b+c)\)ということが言えます。
共通因数でくくるとは言われますが、ちょっと見方を変えると掛け算の理屈だけで因数分解をしているようにも見えます。
掛け算の理屈だと単純な因数分解はやりにくい…
掛け算の理屈を習うのは小学2年生ですが、この掛け算の理屈を使ったやり方は単純な共通因数でくくるときには使わない方が無難です。
単純な共通因数でくくるような因数分解の時は素直に共通因数でくくる方がやりやすいのではないでしょうか。
例えば、\(2x+4y\)を因数分解するときに掛け算の理屈でやってしまうと、難しくなってしまいます。
無理矢理してみると、最初の項は\(2\)が\(x\)個、後の項は\(2\)が\(2y\)個とみます。
つまり、\(2\)が\(x+2y\)個あるので、\(2(x+2y)\)となります。
できないこともないですが、掛け算の理屈を使ったがゆえにややこしくなってしまいましたね。
まとめ
今回の記事では、共通因数でくくるのが分かりにくい因数分解をするときや、共通因数でくくるのが苦手という子におすすめの方法について書いてみました。
使っている理屈そのものは、小学2年生の算数で習った掛け算の理屈です。
意外と掛け算の理屈だけでも、因数分解することってできました。
共通因数でくくるときに、計算過程が複雑になるときにこの理屈は使いやすいことが多いです。
このやり方だと普段している計算する流れに似ているため抵抗が少ないという子もいるかもしれませんね。
