平方根を求めるには素因数分解をすることが基本です。
中には素因数分解をしても平方根を求められないという数もあります。
4の平方根を求めると±2、9の平方根を求めると±3ということは分かりますが、2の平方根はいくらですか、と聞かれると困ってしまいますよね。
今回の記事では、素因数分解で平方根を求められない数の平方根について書いてみたいと思います。
素因数分解では求められない平方根のイメージは?
以前の記事で、平方根を求めるときの基本は素因数分解と紹介しました。
・平方根の求め方って?分数や小数の時はどうしたら良いの?
きちんと平方根が整数や小数、分数できれいに書き切れるときにはこのやり方でいいのですが、問題はきれいな数にならない場合です。
例題を使って考えてみましょう。
まず平方根とはどんな数だったか覚えていますか?
このことをはっきりしておかないと、訳が分からなくなってしまいます。
・平方根の意味とは
2乗するとある数になるものを、その数の平方根といいます。
例えば、\(\pm2\)は2乗すると4になるので、\(\pm2\)は4の平方根だと言えます。
平方根をイメージするときに、「2乗するとある数になるものを、その数の平方根」だと考えていくと、平方根って何なのかイメージがしづらくなります。
平方根をイメージする時には正方形をイメージして考えると、分かりやすくなります。
先ほどの4の平方根が\(\pm2\)ということを正方形を用いてイメージするとこんな感じになります。
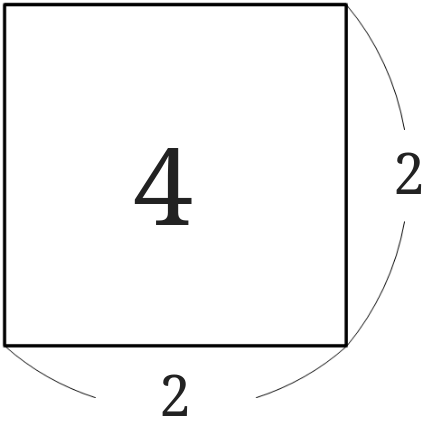 上の図のように、4を正方形の面積として考えてみると、4の平方根である2は正方形の一辺とみることができます。[1] … Continue reading
上の図のように、4を正方形の面積として考えてみると、4の平方根である2は正方形の一辺とみることができます。[1] … Continue reading
このイメージがあると、平方根の単元の理解はしやすくなります。
それでは、正方形を使って、2の平方根を考えてみましょう。
2の平方根なので、正方形の面積は2ということになります。
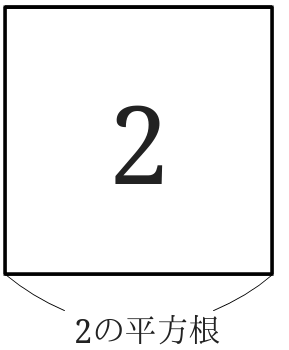 この時の1辺の長さが、2の平方根です。
この時の1辺の長さが、2の平方根です。
2の平方根を求めようとしてみても、求めるのが難しいのです。
一応1と2の間にあるということは分かります。
つまり、2の平方根は\(1.\cdots\)という感じになります。
2の平方根を\(k\)とすると、\(k^2=2\)ということになりますが、これ以上どうにもできそうにありません。
1と2の間にあるということなので、2の平方根を\(\frac{q}{p}\)として考えてみます。
\(p\)と\(q\)は、公約数を1しか持たない自然数とします。
つまり\(\frac{q}{p}\)は約分ができない分数ということです。\(\frac{q}{p}\)は、2の平方根なので、$$(\frac{q}{p})^2=2$$となります。
ここで一つ問題が出てしまいました。
\(p\)と\(q\)の公約数は1なので、\(\frac{q}{p}\)は約分できないことになります。
\(\frac{q}{p}\)が分数にならいのは、\(p=1\)の場合だけです。
またそのとき、\(q^2=2\)をみたすことのできる自然数はありません。
\(p\neq 1\)のとき、\( (\frac{q}{p})^2\)は分数になります。[2] \(p\)と\(q\)は公約数を1以外に持たないので、約分できません。\( (\frac{q}{p})^2=2\)を満たせる\(p\)と\(q\)は存在しないということになります。[3]\( … Continue reading
と、いうことは分数で2の平方根は書き表せないということを意味します。
困りましたね。
ただ、面積が2の正方形は存在しますし、さらにその一辺の長さが2の平方根ということはその数自体は存在するはずです。
分数で表せないということは小数で書いても循環しないということになるので、きちんと書くのは難しいです。
そこで、2の平方根を\(\sqrt{2}\)[4]読み方はルート2と読みます。と書くことにしました。
不規則に続く小数なので記号をつくっちゃったんですね。
円周率の\(\pi\)みたいですね。
2の平方根を\(\sqrt{2}\)と書いたので、\(\sqrt{2}\times \sqrt{2}=2\)となることがすっと出るようになっておくとばっちりですね。
ちなみに2の平方根は\(\pm\sqrt{2}\)となります
まとめ
今回の記事では、素因数分解で平方根を求められない数の平方根について書いてみました。
きちんと平方根が整数の整数で表せるモノであれば素因数分解を使って求めることができるのですが、表せないときは、√を使って表します。
3の平方根は\(\pm\sqrt{3}\)という感じで表せるようになっておけばOKです。
正方形を使って平方根のイメージができると取っつきやすくなるかもしれませんね。




