等積変形って面白い性質ですよね。
中学生でこれを習うと何かと等積変形したがる子がちょこちょこいます。
面白い子は「等積変形で何が出来るかなぁ」と等積変形をしまくっている子もいました。
さて、今回は等積変形の理屈を用いて、元の三角形の面積が2倍となる三角形の書き方を紹介します。
等積変形のポイント
等積変形を使った応用問題の解き方の前に等積変形をきちんと理解しておきましょう。
きちんと理解しないとどうしても、単純な解法の暗記になってしまいます。
単純な暗記のデメリットはすぐ忘れちゃうと言うことです。
数学って暗記量が圧倒的に少ない科目なのになかなか解けるようになりませんよね。
それって理解が伴っていないことから起こることが多いです。
やはりきちんと理解していると忘れにくく、例え忘れたとしてもすぐ思い出すことが出来ますよ。
まずは等積変形の理屈を理解しましょう。
分かっている人は復習気分で見てみてくださいね。
赤い三角形と青い三角形の面積が等しいと言うものでした。
2本の直線は平行ですよ。
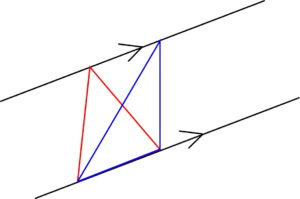
特徴は底辺が共通となっていることです。
高さを書き込むとこんな感じになります。
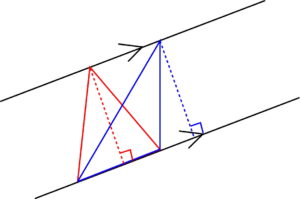
2直線は平行なので赤い三角形と青い三角形の高さは等しいと言うことになります。
三角形の面積\(=\)底辺\(\times \)高さ\(\div 2\)なので、底辺と高さが等しい三角形は面積が等しいと言えます。
まずはここまで理解してくださいね。
等積変形を使った面積が2倍の三角形の書き方
等積変形は面積が等しい三角形の書き方であると同時に、底辺と高さが等しい三角形の書き方とも見ることができます。
底辺が共通ということを利用して面積が2倍の三角形の書き方を考えてみます。
始めの図を使って考えてみます。

直線\(l\)と直線\(m\)が平行なので赤い三角形と青い三角形の面積が等しかった訳です。
ということは、高さを2倍にすれば面積も2倍になります。
2倍の高さを描くには、2本の平行線同士の距離が2倍になれば高さも2倍になります。
こんな感じの直線になります。

底辺が共通でもう一点を今引いた直線上にとれば面積が2倍になります。
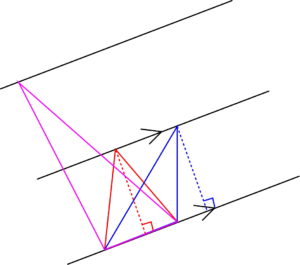
これで元の三角形の2倍の三角形を描くことが出来ますね。[1]高さを3倍にすれば元の三角形の3倍の面積が描けます。高さを\(\frac{1}{2}\)倍にすれば面積も\(\frac{1}{2}\)になります。
これで面積が2倍の三角形を描くことが出来るようになったのですが、このことをどのように使えばいいのかを次に説明します。
等積変形を使った応用問題
等積変形を使って、元の三角形の2倍の面積の三角形をどのようなときに使えるのか見ていきましょう。
簡単な例で見ていきますよ。
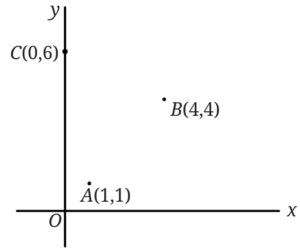
図のように\(A(1,1),B(4,4),C(0,6)\)の3点があります。
\(x\)軸上に点\(P\)をとり\(\triangle ABC\)の2倍の\(\triangle ABP\)を作るとき点\(P\)の座標を求めましょう。
 それでは求めてみましょう。
それでは求めてみましょう。
まずは直線\(AB\)を引き、直線\(AB\)に平行で点\(C\)を通る直線(これ以降、直線\(C\)と書きます。)を引きます。
 さらに直線\(C\)から直線\(AB\)と直線\(C\)と同じ距離にある直線\(D\)を書きます。
さらに直線\(C\)から直線\(AB\)と直線\(C\)と同じ距離にある直線\(D\)を書きます。
どこに直線\(D\)を引くのかというと、この時は\(y\)軸上の点に着目します。
直線\(AB\)は原点を通る直線です。点\(C\)の座標は\( (0,6)\)。
直線\(D\)は、点\( (0,12)\)を通る直線になります。
 この直線の式は直線\(AB\)に平行なので\(y=x+12\)となります。
この直線の式は直線\(AB\)に平行なので\(y=x+12\)となります。
よって、点\(P\)の座標は\( (-12,0)\)と言うことになります。[2]きちんと求めるともう1つ点\(P\)はありますがここでは無しでいきたいと思います。一応書いておくと\(y=x-12\)と\(x\)軸の交点の\( … Continue reading
単純に見ると高校入試ではこんな感じで出てきます。
等積変形を使った高校入試の問題
<例題>
\(y=x^2\)の放物線上に\(x\)座標が\(-1\)の点\(A\)と\(x\)座標が\(2\)の点\(B\)があります。
放物線\(y=x^2\)上に点\(P\)をとり、\(\triangle ABP\)が\(\triangle OAB\)の面積の2倍の面積になるようにするとき点\(P\)の座標を求めましょう。
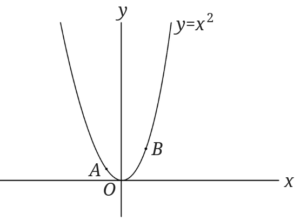 まずは点\(A\)と点\(B\)の座標を求めます。
まずは点\(A\)と点\(B\)の座標を求めます。
それぞれ\(x\)座標が与えられているので、\(y=x^2\)に代入して求めます。
すると、点\(A\)と点\(B\)の座標はそれぞれ\( (-1,1),(2,4)\)となります。
さらに直線\(AB\)を求めると\(y=x+2\)となります。
点\(O\)を通り直線\(AB\)に平行な直線を求めると\(y=x\)となります。
\(y=x+2\)から\(y=x\)と\(y=x+2\)の距離が2倍である直線は\(y=x+6\)と\(y=x-2\)となります。
\(y=x-2\)の直線は\(y=x^2\)と交点がないので無視します。
\(y=x+6\)と\(y=x^2\)を連立して交点を出します。
\(\begin{eqnarray} \left\{ \begin{array}{l} y=x+6 \\ y=x^2 \end{array} \right.\end{eqnarray}\)
これを解くと\(x=-2,3\)
\(x=-2,3\)を\(y=x+6\)に代入して\(y\)座標を求めます。
求める点\(P\)の座標は、\( (-2,4)\)と\( (3,9)\)となります。
まとめ
今回は等積変形を用いて元の三角形の2倍の三角形の作図や求め方を紹介しました。
等積変形が面積が等しい三角形の作図だっものから、この考え方が出来るようになると、随分といろいろな面積の三角形の作図などが出来るようになります。
等積変形の根本的な理屈が飲み込めていればすんなり使えるのではないでしょうか。
等積変形の理屈がよく分からないなぁと言うときはまずは等積変形をしっかり理解しましょう。
遠いようで意外と近道になります。
面倒くさがらずに頑張って理解しましょう。





高校入試の問題は点Pはあと4つありますね。(―2,4)(3,9) (―3,9)(4,16)です。
コメントありがとうございます。
そもそも求めるものを間違えておりました。
ご指摘ありがとうございました。